阅读数 nan

马 拉 车

引入

给定一个字符串 $s$，求它的最长回文子串的长度。$|s|\le 10^7$

我们需要找到一种线性解法，那就是 $\text{Manacher}$。

算法流程

首先回顾回文串的定义，即正序和倒序的字符串一模一样，如 $\texttt{abcba}$。

不难发现每个回文串都有一个对称中心，有时是一个确定的字符，有时对称位不在字符上（长度为偶数）。

因此为了方便，在每两个字符之间加一个相同的字符，这样对称位一定在字符上。

求解时要借助 $p[],mid,mx$，$p_i$ 表示以 $i$ 为中心的向一个方向的延伸的最长长度而不是整个回文串的长度，或者可理解为 $p_i=\dfrac{len+1}{2}$。

不难发现最终的答案为 $\max(p_i)-1$，那么问题转化为求解 $p$。

那我们先继续说剩下两个：$mx$ 表示**当前的回文串中出现的最右端 $+1$**，$mid$ 表示 $mx$ 出现的最远的对称中心 。

然后我们枚举 $i$ 并分类讨论：

① 当 $i$ 在 $mid$ 和 $mx$ 之间，作出 $i$ 关于 $mid$ 的对称点 $j$。

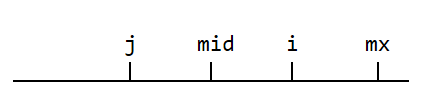
假设以 $j$ 为对称中心的最长回文子串为红色部分，那么以 $i$ 为对称中心的最长回文子串一定为相应的紫色部分且不会更长，这个由对应的定义可以证明。

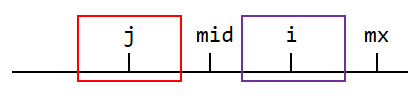
那如果出现这种情况？

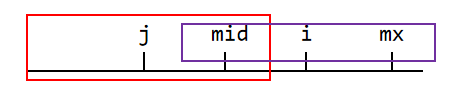
因为当前的只判断到 $mx$ 以前，超过的部分需要充重新判断，这块直接暴力比对即可。

② 当 $i$ 超过 $mx$ 时，重新从最小开始比较即可。

当当前判断到的位置超过 $mx$ 时，更新一下新的 $mx$ 和 $mid$ 即可。

复杂度分析

因为判断过的位置不会再重复判断，所以是线性的复杂度。

代码

int n, p[maxn];
char s[maxn];
void manacher() {
    int mid = 1, mx = 0;
    s[0] = '!', s[1] = '|';
    for(int i = 1;i <= n;i++) {
        s[i * 2] = ss[i], s[i * 2 + 1] = '|';
    }
    s[n * 2 + 2] = '?';
    for(int i = 1;i <= 2 * n + 1;i++) {
        if(mx > i) {
            p[i] = min(p[2 * mid - i], mx - i);
        }
        else {
            p[i] = 1;
        }
        while(s[i + p[i]] == s[i - p[i]]) p[i]++;
        if(i + p[i] > mx) {
            mx = i + p[i], mid = i;
        }
    }
}