引入
给定长度为 $n$ 的字符串,请把这个字符串的所有 $n$ 个非空后缀按字典序(用 ASCII 数值比较)从小到大排序,然后按顺序输出排名。位置编号为 $1$ 到 $n$。
对于 $100%$ 的数据,$n\le10^6$。
暴力怎么做?暴力是不是,加边,加边,加边,然后,并查集查询。
不难想到用 $\text{sort}$ 进行排序,我们可以用哈希和二分优化,复杂度 $O(n\log^2n)$。
对于一般的题目,暴力与正解往往有所关联,但是…
好了,下面正式开始介绍算法。
定义
记 $suf(i)$ 表示字符串 $s[i, n]$ 所对应的子串,同时也称以 $n$ 为结尾的子串为字符串的后缀。
定义 $SA_i$ 表示排名第 $i$ 的后缀的开始位置。$SA_i$ 建立的是 “排名 $\rightarrow$ 位置” 映射关系。
定义 $rk_i$ 表示 $suf(i)$ 这个后缀在所有后缀中的字典序排名。$rk_i$ 建立的是 “位置 $\rightarrow$ 排名” 映射关系。
算法流程
我们采用的是倍增思想,如需对字符串 $s=\texttt{abcaabc}$ 排序。
首先我们先对每个后缀的前 $1$ 位进行比较,若相等则他们的排名一样。

然后比较前 $2$ 位时,我们就可以用两个连续的 $1$ 位字符拼接,这样每一位就有了一个二元组,然后我们用二元组排名。

注意,如果没有完整的话就补 $0$。
然后继续比较前 $4$ 位。

这时你突然发现,好像所有位置的排名都不一样了!那么算法就结束了。
代码(全文背诵)
在具体实现时,对二元组排序我们采用基数排序,先排第二维后排第一维,排序复杂度 $\mathcal{O}(n\log n)\rightarrow \mathcal{O}(n)$,加上倍增总时间复杂度为 $\mathcal{O}(n\log n)$,一般情况下足够使用。而因为常数较大,代码进行了卡常操作,因此部分实现原理可能并不显然,推荐采用理解思路+记忆细节的方式完成代码。(作者暂时也并未深究)
进行压行处理后 suffixArray() 函数仅有 $20$ 行,十分容易记忆,一定要全文背诵!一定要全文背诵!一定要全文背诵!
int sa[1000005], rk[2000005]; // 注意 rk 和 oldrk 需要开 2 倍字符串长度。
int cnt[1000005], id[1000005], px[1000005], oldrk[2000005];
inline bool cmp(int x, int y, int j) {
return (oldrk[x] == oldrk[y] && oldrk[x + j] == oldrk[y + j]);
}
void suffixArray() {
m = max(n, 300);
int i, j, t;
for(i = 1; i <= n; ++i) ++cnt[rk[i] = str[i]];
for(i = 1; i <= m; ++i) cnt[i] += cnt[i - 1];
for(i = n; i >= 1; --i) sa[cnt[rk[i]]--] = i;
for(j = 1; j < n; j <<= 1, m = t) {
for(t = 0, i = n; i > n - j; --i) id[++t] = i;
for(i = 1; i <= n; ++i)
if(sa[i] > j) id[++t] = sa[i] - j;
memset(cnt, 0, sizeof cnt);
for(i = 1; i <= n; ++i) ++cnt[px[i] = rk[id[i]]];
for(i = 1; i <= m; ++i) cnt[i] += cnt[i - 1];
for(i = n; i >= 1; --i) sa[cnt[px[i]]--] = id[i];
memcpy(oldrk, rk, sizeof oldrk);
for(t = 0, i = 1; i <= n; ++i)
rk[sa[i]] = cmp(sa[i], sa[i - 1], j) ? t : ++t;
if(t == n) break;
}
}
小建议:不要在做题时直接套用模板,每一次都要认真手打。我的真实体验是做 $3$ 道题就能完全自己写对模板。
$\text{Height}$
假设现在给你这么一道题:在 $\mathcal{O}(n\log n)-\mathcal{O}(1)$ 的复杂度求出 $\text{lcp}(suf(i), suf(j))$,很显然你想不到这和 SA 有什么关系,那么接下来我们引入新定义。
记 $height_i$ 表示 $suf(SA_i)$ 与 $suf(SA_{i-1})$ 的最长公共前缀长度,即 $\text{lcp}(suf(SA_i), suf(SA_{i-1}))$,那么有结论:
$\text{lcp}(suf(i),suf(j))=\min\limits_{rk_i<k\leq rk_j}height_k$,这里假设 $rk_i<rk_j$,那么为什么有这个结论呢,我们需要证明:
记 $s_1=suf(i),s_2=suf(j),s_3=suf(k)$。
有 $\forall s_1<s_2<s_3,\text{ s.t. } \text{lcp}(s_1,s_3)=\min(\text{lcp}(s_1,s_2),\text{lcp}(s_2,s_3))$。
对于这个命题,我们只需分类讨论即可。大致根据 $\text{lcp}(s_1,s_2)$ 和 $\text{lcp}(s_2,s_3)$ 的大小关系分为 $3$ 种简单的小情况:
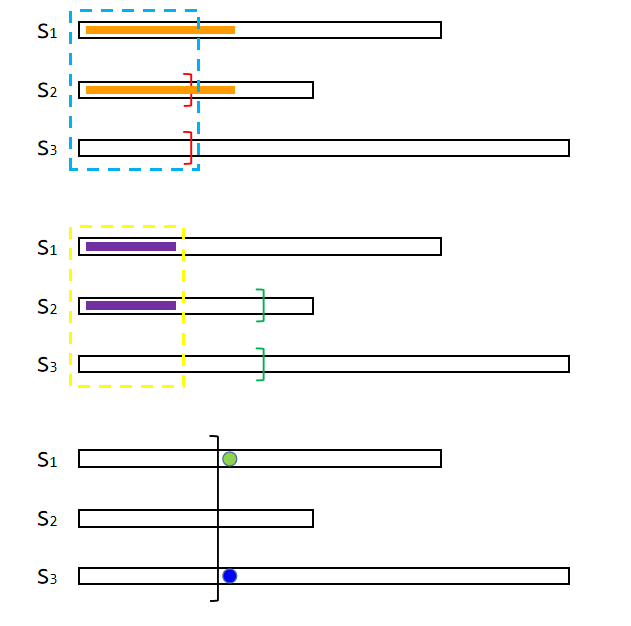
上图分别对应 $\text{lcp}(s_1,s_2)>\text{lcp}(s_2,s_3)$,$\text{lcp}(s_1,s_2)<\text{lcp}(s_2,s_3)$ 和 $\text{lcp}(s_1,s_2)=\text{lcp}(s_2,s_3)$ 的情况。
特别说明 $\text{lcp}(s_1,s_2)=\text{lcp}(s_2,s_3)$ 的情况,因为 $s_1<s_2<s_3$,所以 $s_1$ 和 $s_3$ 下一个字符不能相同,因此满足 $\text{lcp}(s_1,s_3)=\min(\text{lcp}(s_1,s_2),\text{lcp}(s_2,s_3))$。
那么任意两个后缀,它们的最长公共前缀就成了 $height$ 上的 RMQ 问题,因此能 $\mathcal{O}(n\log n)-\mathcal{O}(1)$ 解决。
新的问题:如何求出 $\text{Height}$ 数组
不要高兴太早,现在我们还需要以较低的复杂度求出 $\text{Height}$ 数组。
暴力 $\mathcal{O}(n^2)$ 留给读者思考,我们接下来证明下一个结论:
$\forall i\in[1,n],\text{ s.t. }height_{rk_i}\geq height_{rk_{i-1}}-1$
我们考虑 $suf(k)$ 与 $suf(i-1)$ 的最长公共前缀,$suf(k)$ 表示在按字典序顺序排在 $suf(i-1)$ 的前一个的后缀,此时最长公共前缀显然为 $height_{rk_{i-1}}$。
分情况讨论一下:
$suf(k)$ 与 $suf(i-1)$ 的首字母不相同,那么此时 $height_{rk_{i-1}}=0$,一定有 $height_{rk_i}\geq 0>height_{rk_{i-1}}$。
$suf(k)$ 与 $suf(i-1)$ 的首字母相同,此时我们有必要讨论 $suf(k+1)$ 与 $suf(i)$ 的关系。
观察到两个后缀均去掉了首字母,得 $\text{lcp}(suf(k+1),suf(i))=height_{rk_{i-1}}-1$。
又因为 $suf(k)$ 的排名小于 $suf(i-1)$,则去掉首字母的排名 $suf(k+1)$ 小于 $suf(i)$,那么根据上面刚证明的结论,一定有:
$\text{lcp}(suf(rk_i-1),suf(i))\geq \text{lcp}(suf(k+1),suf(i))$,代入整理后可得:
$hright_{rk_i}\geq height_{rk_{i-1}}-1$。
综上,任何情况下,都有 $height_{rk_i}\geq height_{rk_{i-1}}-1$。
代码实现
那么现在我们只需按 $rk_1\sim rk_n$ 顺序求 $height$ 数组,根据摊还分析,复杂度就是 $\mathcal{O}(n)$。
for(i = 1; i <= n; ++i) {
j = sa[rk[i] - 1];
int k = max(0, height[rk[i - 1]] - 1);
while(str[i + k] == str[j + k]) ++k;
height[rk[i]] = k;
}
现在你已点亮了关于 SA 的所有技能点!(SAM 应该还有新的)
下面你就可以快乐的刷题,大部分题用完 SA 后会转化为另一道可出在联赛的题目。
习题
注意下文中复杂度的 $n$ 均指进行 SA 的字符串长度。貌似复杂度都一样
P3809 【模板】后缀排序
直接上 SA 板子即可,最后输出的即为 $SA$ 数组。
时间复杂度 $\mathcal{O}(n\log n)$。
P2870 [USACO07DEC]Best Cow Line G
观察到字典序具有贪心性,考虑从两个中选择令答案较优的那个,具体来说:
设当前字符串剩余 $s[l,r]$,那么如何决策选择 $l$ 还是 $r$?
当 $s_l$ 和 $s_r$ 不一样时,根据贪心我们选择较小的那个。
如果一样时,我们就得根据 $s_{l+1}$ 和 $s_{r-1}$ 来决策选择 $s_l$ 还是 $s_r$,如果还是相同就继续比较 $s_{l+2}=s_{r-2}$,最后直到比较出大小为止。
观察到这一过程就是在比较 $l\rightarrow r$ 和 $r\rightarrow l$ 这两段字符的字典序排名。
我们将原串倒过来,使用后缀数组,这样就有了原串后缀和原串前缀的排名,按上述流程操作时比较 $rk$ 即可。
时间复杂度 $\mathcal{O}(n\log n)$。代码是远古时期(2021-12-14)写的,就不放了。
P2408 不同子串个数
给定一个长为 $n$ 的字符串,求不同的子串个数。
观察到 $height_i=\text{lcp}(suf(sa_i),suf(sa_{i-1}))$,那么对于 $suf(sa_i)$ 和 $suf(s_{i-1})$ 来说,有长度 $height_i$ 的公共部分,也就是有 $height_i$ 个重复子串,那么最终答案即为:$\dfrac{n(n+1))}{2}-\sum\limits_{i=1}^n height_i$。
时间复杂度 $\mathcal{O}(n\log n)$。
代码
#include <bits/stdc++.h>
using namespace std;
typedef long long ll;
int n, m;
char str[100005];
int sa[100005], rk[200005], height[100005];
int id[100005], cnt[100005], px[100005], oldrk[200005];
inline bool cmp(int x, int y, int j) {
return (oldrk[x] == oldrk[y] && oldrk[x + j] == oldrk[y + j]);
}
void suffixArray() {
m = max(n, 300);
int i, j, t;
for(i = 1; i <= n; ++i) ++cnt[rk[i] = str[i]];
for(i = 1; i <= m; ++i) cnt[i] += cnt[i - 1];
for(i = n; i >= 1; --i) sa[cnt[rk[i]]--] = i;
for(j = 1; j < n; j <<= 1, m = t) {
for(t = 0, i = n; i > n - j; i--) id[++t] = i;
for(i = 1; i <= n; ++i)
if(sa[i] > j) id[++t] = sa[i] - j;
memset(cnt, 0, sizeof cnt);
for(i = 1; i <= n; ++i) ++cnt[px[i] = rk[id[i]]];
for(i = 1; i <= m; ++i) cnt[i] += cnt[i - 1];
for(i = n; i >= 1; --i) sa[cnt[px[i]]--] = id[i];
memcpy(oldrk, rk, sizeof oldrk);
for(t = 0, i = 1; i <= n; ++i)
rk[sa[i]] = cmp(sa[i], sa[i - 1], j) ? t : ++t;
if(t == n) break;
}
for(i = 1; i <= n; ++i) {
j = sa[rk[i] - 1];
int k = max(0, height[rk[i - 1]] - 1);
while(str[i + k] == str[j + k]) ++k;
height[rk[i]] = k;
}
}
int main() {
ios::sync_with_stdio(false);
cin.tie(nullptr), cout.tie(nullptr);
cin >> n >> (str + 1);
suffixArray();
ll sum = (ll)n * (n + 1) / 2;
for(int i = 1; i <= n; ++i) {
sum -= height[i];
}
cout << sum << '\n';
cout.flush();
return 0;
}
P2852 [USACO06DEC]Milk Patterns G
这题考查了一点关于 $\text{Height}$ 的应用。
我们思考 $\text{Height}$ 的定义,是排名相邻的两个串的最长公共前缀,而由于后缀按字典序排名后,具有一段相同前缀的字符串必定是挨在一起的!

那么我们可以二分一个长度 $l$,把 $height_i<l$ 的位置称之为 “断点”,这样所有后缀被我们分成了若干组,可以证明每个后缀的相同一段前缀在原字符串上的位置是不同的。
那么我们看是否有一组的数量到达 $k$ 即可。时间复杂度 $\mathcal{O}(n\log n)$。
有了这种想法后我们发现可以完全不用二分。我们对相邻的 $k$ 个对应的 $(k-1)$ 个 $height_i$ 取最小值就是相邻 $k$ 个的贡献的答案,最终所有答案求最大值即可。用单调队列维护,复杂度为 $\mathcal{O}(n)$,但由于求 SA 的瓶颈,复杂度仍为 $\mathcal{O}(n\log n)$。
P5546 [POI2000]公共串
这题展现了关于 SA 做题的另一技巧。
观察到最长公共子串显然是可以 SA 求的,但是不在一个字符串啊,只有在一个字符串上才能进行排名。
不难想到将所有字符串拼接起来并在字符串之间加一个未出现字符,此时再进行排序我们就有了所有字符串的所有后缀的字典序关系。
然后双指针更新答案即可,我们要保证区间内包含了所有字符串的后缀至少一个。时间复杂度 $\mathcal{O}(n\log n)$。
代码
#include <bits/stdc++.h>
using namespace std;
int n, m, q;
int str[10105];
char Tmp[2005];
int pos[10105], bucket[10], tot;
int lg2[10105], st[10105][15];
int sa[10105], rk[20205], height[10105];
int id[10105], cnt[10105], px[10105], oldrk[20205];
inline bool cmp(int x, int y, int j) {
return (oldrk[x] == oldrk[y] && oldrk[x + j] == oldrk[y + j]);
}
void suffixArray() {
m = max(n, 300 + q);
int i, j, t;
for(i = 1; i <= n; ++i) ++cnt[rk[i] = str[i]];
for(i = 1; i <= m; ++i) cnt[i] += cnt[i - 1];
for(i = n; i >= 1; --i) sa[cnt[rk[i]]--] = i;
for(j = 1; j < n; j <<= 1, m = t) {
for(t = 0, i = n; i > n - j; --i) id[++t] = i;
for(i = 1; i <= n; ++i)
if(sa[i] > j) id[++t] = sa[i] - j;
memset(cnt, 0, sizeof cnt);
for(i = 1; i <= n; ++i) ++cnt[px[i] = rk[id[i]]];
for(i = 1; i <= m; ++i) cnt[i] += cnt[i - 1];
for(i = n; i >= 1; --i) sa[cnt[px[i]]--] = id[i];
memcpy(oldrk, rk, sizeof oldrk);
for(t = 0, i = 1; i <= n; ++i)
rk[sa[i]] = cmp(sa[i], sa[i - 1], j) ? t : ++t;
if(t == n) break;
}
for(i = 1; i <= n; ++i) {
j = sa[rk[i] - 1];
int k = max(0, height[rk[i - 1]] - 1);
while(str[i + k] == str[j + k]) ++k;
height[rk[i]] = k;
}
}
int que(int l, int r) {
if(l > r) return 0;
int j = lg2[r - l + 1];
return min(st[l][j], st[r - (1 << j) + 1][j]);
}
int main() {
ios::sync_with_stdio(false);
cin.tie(nullptr), cout.tie(nullptr);
cin >> q;
for(int j = 1; j <= q; ++j) {
cin >> (Tmp + 1);
for(int i = 1, l = strlen(Tmp + 1); i <= l; ++i) {
str[++n] = Tmp[i]; pos[n] = j;
}
str[++n] = 127 + j;
}
suffixArray();
lg2[0] = -1;
for(int i = 1; i <= n; ++i) {
lg2[i] = lg2[i / 2] + 1;
}
for(int i = 1; i <= n; ++i) {
st[i][0] = height[i];
}
for(int j = 1; (1 << j) <= n; ++j) {
for(int i = 1; i + (1 << j) - 1 <= n; ++i) {
st[i][j] = min(st[i][j - 1], st[i + (1 << (j - 1))][j - 1]);
}
}
int res = 0;
for(int i = 1, j = 1; i <= n; ++i) {
while(j <= n && tot < q) {
if(bucket[pos[sa[j]]] == 0) tot++;
bucket[pos[sa[j]]]++, j++;
}
res = max(res, que(i + 1, j - 1));
if(bucket[pos[sa[i]]] == 1) tot--;
bucket[pos[sa[i]]]--;
}
cout << res << '\n';
cout.flush();
return 0;
}
P4248 [AHOI2013] 差异
本题实际上又是个一眼题。
$\text{len}$ 的贡献显然是好算的,每个 $\text{len}(suf(i))$ 贡献 $(n-1)$ 次,所以所有的贡献加起来为 $\dfrac{(n-1)\cdot n\cdot (n+2)}{2}$。
接下来考虑计算 $\sum\limits_{i<j}\text{lcp(suf(i),suf(j))}$,实际上这就是对区间最小值进行求和,那么我们要找到每一个 $height_i$ 第一个左边比它大的位置 $L_i$ 和第一个右边比它大的位置 $R_i$,那么 $height_i$ 的贡献就是 $height_i\times (i-L_i)\times(R_i-i)$。注意还要乘上题目式子中的 $2$。
求出 $L_i$ 和 $R_i$ 是一个使用单调栈维护的经典问题,不作赘述。
时间复杂度 $\mathcal{O}(n\log n)$。
代码
#include <bits/stdc++.h>
using namespace std;
typedef long long ll;
int n, m;
char str[500005];
int sa[500005], rk[1000005], height[500005];
int id[500005], cnt[500005], px[500005], oldrk[1000005];
inline bool cmp(int x, int y, int j) {
return (oldrk[x] == oldrk[y] && oldrk[x + j] == oldrk[y + j]);
}
void suffixArray() {
m = max(n, 300);
int i, j, t;
for(i = 1; i <= n; ++i) ++cnt[rk[i] = str[i]];
for(i = 1; i <= m; ++i) cnt[i] += cnt[i - 1];
for(i = n; i >= 1; --i) sa[cnt[rk[i]]--] = i;
for(j = 1; j < n; j <<= 1, m = t) {
for(t = 0, i = n; i > n - j; --i) id[++t] = i;
for(i = 1; i <= n; ++i)
if(sa[i] > j) id[++t] = sa[i] - j;
memset(cnt, 0, sizeof cnt);
for(i = 1; i <= n; ++i) ++cnt[px[i] = rk[id[i]]];
for(i = 1; i <= m; ++i) cnt[i] += cnt[i - 1];
for(i = n; i >= 1; --i) sa[cnt[px[i]]--] = id[i];
memcpy(oldrk, rk, sizeof oldrk);
for(t = 0, i = 1; i <= n; ++i)
rk[sa[i]] = cmp(sa[i], sa[i - 1], j) ? t : ++t;
if(t == n) break;
}
for(i = 1; i <= n; ++i) {
j = sa[rk[i] - 1];
int k = max(0, height[rk[i - 1]] - 1);
while(str[i + k] == str[j + k]) ++k;
height[rk[i]] = k;
}
}
int stac[500005], top;
int L[500005], R[500005];
int main() {
ios::sync_with_stdio(false);
cin.tie(nullptr), cout.tie(nullptr);
cin >> (str + 1);
n = strlen(str + 1);
suffixArray();
for(int i = 2; i <= n; ++i) {
L[i] = 1, R[i] = n + 1;
}
for(int i = 2; i <= n; ++i) {
while(top > 0 && height[stac[top]] > height[i]) {
R[stac[top]] = i, top--;
}
if(top > 0) L[i] = stac[top];
stac[++top] = i;
}
ll ans = (ll)n * (n + 1) / 2 * (n - 1);
for(int i = 2; i <= n; ++i) {
ans -= (ll)height[i] * (i - L[i]) * (R[i] - i) * 2;
}
cout << ans << '\n';
cout.flush();
return 0;
}
P2463 [SDOI2008] Sandy 的卡片
本题中需要注意相同子串的定义:两个子串长度相同且一个串的全部元素加上一个数就会变成另一个串。
那么我们可以将每个串的差分求出来,然后依次拼接,按 P5546 [POI2000]公共串 的方法求出来的答案加 $1$ 就是本题答案。
时间复杂度 $\mathcal{O}(n\log n)$。
CF204E Little Elephant and Strings
我们先把所有包含恰好 $k$ 个串的后缀所在的排名区间找到,那么一个后缀对其所在串的贡献就是此后缀所在的所有区间 $\text{height}$ 最小值中的最大值。那么找到了所有区间后,我们考虑依次对每个后缀维护答案。
不难发现区间左右指针单调(非严格)递增,因此相当于维护滑动窗口区间最大值,用单调队列即可。
时间复杂度 $\mathcal{O}(n\log n)$。
代码
#include <bits/stdc++.h>
using namespace std;
typedef long long ll;
int n, m, q, k;
int str[200005], lst[200005];
char Tmp[200005];
vector<pair<int, int>> adj[200005];
int pos[200005], bucket[200005], tot;
pair<int, int> que[200005];
int head, tail;
int lg2[200005], st[200005][20];
int sa[200005], rk[400005], height[200005];
int id[200005], cnt[200005], px[200005], oldrk[400005];
ll sum[200005];
inline bool cmp(int x, int y, int j) {
return (oldrk[x] == oldrk[y] && oldrk[x + j] == oldrk[y + j]);
}
void suffixArray() {
m = max(n, 300 + q);
int i, j, t;
for(i = 1; i <= n; ++i) ++cnt[rk[i] = str[i]];
for(i = 1; i <= m; ++i) cnt[i] += cnt[i - 1];
for(i = n; i >= 1; --i) sa[cnt[rk[i]]--] = i;
for(j = 1; j < n; j <<= 1, m = t) {
for(t = 0, i = n; i > n - j; --i) id[++t] = i;
for(i = 1; i <= n; ++i)
if(sa[i] > j) id[++t] = sa[i] - j;
memset(cnt, 0, sizeof cnt);
for(i = 1; i <= n; ++i) ++cnt[px[i] = rk[id[i]]];
for(i = 1; i <= m; ++i) cnt[i] += cnt[i - 1];
for(i = n; i >= 1; --i) sa[cnt[px[i]]--] = id[i];
memcpy(oldrk, rk, sizeof oldrk);
for(t = 0, i = 1; i <= n; ++i)
rk[sa[i]] = cmp(sa[i], sa[i - 1], j) ? t : ++t;
if(t == n) break;
}
for(i = 1; i <= n; ++i) {
j = sa[rk[i] - 1];
int k = max(0, height[rk[i - 1]] - 1);
while(str[i + k] == str[j + k]) ++k;
height[rk[i]] = k;
}
}
int query(int l, int r) {
if(l > r) return lst[pos[sa[r]]] - sa[r] + 1;
int j = lg2[r - l + 1];
return min(st[l][j], st[r - (1 << j) + 1][j]);
}
int main() {
ios::sync_with_stdio(false);
cin.tie(nullptr), cout.tie(nullptr);
cin >> q >> k;
for(int j = 1; j <= q; ++j) {
cin >> (Tmp + 1);
for(int i = 1, l = strlen(Tmp + 1); i <= l; ++i) {
str[++n] = Tmp[i]; pos[n] = j;
}
lst[j] = n;
str[++n] = 300 + j;
}
suffixArray();
for(int i = 1; i <= n; ++i) {
st[i][0] = height[i];
}
lg2[0] = -1;
for(int i = 1; i <= n; ++i) {
lg2[i] = lg2[i / 2] + 1;
}
for(int j = 1; (1 << j) <= n; ++j) {
for(int i = 1; i + (1 << j) - 1 <= n; ++i) {
st[i][j] = min(st[i][j - 1], st[i + (1 << (j - 1))][j - 1]);
}
}
for(int i = 1, j = 1; i <= n; ++i) { // 求出所有恰好包含 k 个串的后缀的区间 [l, r]
if(bucket[pos[sa[i]]] == 0) tot++;
bucket[pos[sa[i]]]++;
while(tot >= k) {
if(tot == k) {
adj[j].push_back(make_pair(i, query(j + 1, i))); // 保存区间 [j, i]
}
if(bucket[pos[sa[j]]] == 1) {
if(tot == k) break;
tot--;
}
bucket[pos[sa[j]]]--; j++;
}
}
head = 1, tail = 0;
for(int i = 1; i <= n; ++i) {
while(head <= tail && que[head].first < i) ++head;
for(auto p: adj[i]) {
while(head <= tail && que[tail].second < p.second) --tail;
que[++tail] = p;
}
if(head <= tail) {
sum[pos[sa[i]]] += que[head].second;
}
}
for(int i = 1; i <= q; ++i) {
cout << sum[i] << ' ';
}
cout << '\n';
cout.flush();
return 0;
}
P2178 [NOI2015] 品酒大会
求完 SA 后,先考虑如何求方案数。
我们先考虑恰好是 “$k$ 相似” 的方案是多少,如果能求,那么做后缀和后就得到答案数组。
注意到 $\text{lcp}(suf(i),suf(j))$ 是区间最小值 $\text{Height}$ 的形式,那么第一反应到离线涨水+并查集维护的做法。
具体来说,维护并查集表示其中一部分后缀,并同时维护并查集大小。
按 $\text{Height}$ 从大到小倒序合并,当我们合并到 $k$ 时,所有 $k+1\sim n$ 的连续后缀已经合并完成。
那么当我们找到 $Height_i=k$ 时,把 $suf(sa_i)$ 后缀和 $suf(sa_{i+1})$ 后缀所在的并查集合并起来,方案数贡献大小就是两个并查集大小相乘,这样我们就能维护全部方案。
这样的话最大美味度也能维护,但注意到美味度有负数,需要同时维护并查集内最大值和最小值,贡献时最小值$\times$最小值和最大值$\times$最大值都能贡献。
时间复杂度 $\mathcal{O}(n\log n)$。
代码
#include <bits/stdc++.h>
using namespace std;
typedef long long ll;
int n, m;
char str[300005];
int a[300005];
vector<int> adj[300005];
int sa[300005], rk[600005], height[300005];
int id[300005], cnt[300005], px[300005], oldrk[600005];
int fa[300005], sz[300005], Min[300005], Max[300005];
ll sum[300005], seq[300005];
int find(int u) {
if(fa[u] == u) return u;
else return fa[u] = find(fa[u]);
}
void merge(int u, int v, int w) {
int ancu = find(u), ancv = find(v);
sum[w] += (ll)sz[ancu] * sz[ancv];
seq[w] = max(seq[w], max((ll)Min[ancu] * Min[ancv], (ll)Max[ancu] * Max[ancv]));
Min[ancv] = min(Min[ancv], Min[ancu]), Max[ancv] = max(Max[ancv], Max[ancu]), sz[ancv] += sz[ancu], fa[ancu] = ancv;
}
inline bool cmp(int x, int y, int j) {
return (oldrk[x] == oldrk[y] && oldrk[x + j] == oldrk[y + j]);
}
void suffixArray() {
m = max(n, 300);
int i, j, t;
for(i = 1; i <= n; ++i) ++cnt[rk[i] = str[i]];
for(i = 1; i <= m; ++i) cnt[i] += cnt[i - 1];
for(i = n; i >= 1; --i) sa[cnt[rk[i]]--] = i;
for(j = 1; j < n; j <<= 1, m = t) {
for(t = 0, i = n; i > n - j; i--) id[++t] = i;
for(i = 1; i <= n; ++i)
if(sa[i] > j) id[++t] = sa[i] - j;
memset(cnt, 0, sizeof cnt);
for(int i = 1; i <= n; ++i) ++cnt[px[i] = rk[id[i]]];
for(int i = 1; i <= m; ++i) cnt[i] += cnt[i - 1];
for(int i = n; i >= 1; --i) sa[cnt[px[i]]--] = id[i];
memcpy(oldrk, rk, sizeof oldrk);
for(t = 0, i = 1; i <= n; ++i)
rk[sa[i]] = cmp(sa[i], sa[i - 1], j) ? t : ++t;
if(t == n) break;
}
for(i = 1; i <= n; ++i) {
j = sa[rk[i] - 1];
int k = max(0, height[rk[i - 1]] - 1);
while(str[i + k] == str[j + k]) ++k;
height[rk[i]] = k;
}
}
int main() {
ios::sync_with_stdio(false);
cin.tie(nullptr), cout.tie(nullptr);
cin >> n >> (str + 1);
for(int i = 1; i <= n; ++i) {
cin >> a[i];
}
suffixArray();
for(int i = 1; i <= n; ++i) {
fa[i] = i, sz[i] = 1, Min[i] = Max[i] = a[sa[i]];
adj[height[i]].push_back(i);
}
memset(seq, ~0x3f, sizeof(seq));
for(int j = n; j >= 0; --j) {
for(int i: adj[j]) {
merge(i - 1, i, j);
}
}
for(int i = n; i >= 0; --i) {
sum[i] += sum[i + 1], seq[i] = max(seq[i], seq[i + 1]);
}
for(int i = 0; i < n; ++i) {
cout << sum[i] << ' ' << (sum[i] == 0 ? 0 : seq[i]) << '\n';
}
cout.flush();
return 0;
}
P2336 [SCOI2012] 喵星球上的点名
我们把所有串接起来拼 SA,一个喵星人的姓和名之间也要插字符分开。
那么对于一个询问,我们在 SA 中找到极大区间 $[L,R]$ 使得这个区间的最长公共前缀恰好等于询问串长度,那么这就说明这个区间内的所包括的任意一个喵星人都可以在这个询问串下答到。
由于一个喵星人有两个串,不唯一对应,我们将两问转化为如下问题:
- 询问区间 $[L,R]$ 有多少种不同的颜色。
- 询问每种颜色在多少个不同的区间。
如果你做过P1972 [SDOI2009] HH的项链,那么这题就迎刃而解了。
时间复杂度 $\mathcal{O}(n\log n)$。
代码
#include <bits/stdc++.h>
using namespace std;
int n, m, q1, q2;
int Len[400005];
int str[400005], lst[400005], D;
int pre[400005], appear[400005];
int pos[400005];
int lg2[400005], st[400005][20];
int sa[400005], rk[800005], height[400005];
int id[400005], cnt[400005], px[400005], oldrk[800005];
int ans[400005];
vector<pair<int, int>> qu[400005];
vector<int> adj[400005];
int bucket[4000005];
int c[400005];
inline int lowbit(int x) {
return x & (-x);
}
void upd(int x, int v) {
for(int i = x; i <= n; i += lowbit(i)) {
c[i] += v;
}
}
int que(int x) {
int res = 0;
for(int i = x; i > 0; i -= lowbit(i)) {
res+= c[i];
}
return res;
}
inline bool cmp(int x, int y, int j) {
return (oldrk[x] == oldrk[y] && oldrk[x + j] == oldrk[y + j]);
}
void suffixArray() {
m = max(n, 10000 + D);
int i, j, t;
for(i = 1; i <= n; ++i) ++cnt[rk[i] = str[i]];
for(i = 1; i <= m; ++i) cnt[i] += cnt[i - 1];
for(i = n; i >= 1; --i) sa[cnt[rk[i]]--] = i;
for(j = 1; j < n; j <<= 1, m = t) {
for(t = 0, i = n; i > n - j; --i) id[++t] = i;
for(i = 1; i <= n; ++i)
if(sa[i] > j) id[++t] = sa[i] - j;
memset(cnt, 0, sizeof cnt);
for(i = 1; i <= n; ++i) ++cnt[px[i] = rk[id[i]]];
for(i = 1; i <= m; ++i) cnt[i] += cnt[i - 1];
for(i = n; i >= 1; --i) sa[cnt[px[i]]--] = id[i];
memcpy(oldrk, rk, sizeof oldrk);
for(t = 0, i = 1; i <= n; ++i)
rk[sa[i]] = cmp(sa[i], sa[i - 1], j) ? t : ++t;
if(t == n) break;
}
for(i = 1; i <= n; ++i) {
j = sa[rk[i] - 1];
int k = max(0, height[rk[i - 1]] - 1);
while(str[i + k] == str[j + k]) ++k;
height[rk[i]] = k;
}
}
void work(int i, int l) {
int posl = i, posr = i + 1; // height[posl, posr)
if(height[i] >= l) {
for(int j = 19; j >= 0; --j) {
if(posl - (1 << j) >= 2 && st[posl - (1 << j)][j] >= l) {
posl -= (1 << j);
}
}
}
else {
posl = i + 1;
}
if(height[i + 1] >= l) {
for(int j = 19; j >= 0; --j) {
if(posr + (1 << j) - 1 <= n && st[posr][j] >= l) {
posr += (1 << j);
}
}
}
if(posl <= posr) {
qu[posr - 1].push_back(make_pair(posl - 1, pos[sa[i]]));
adj[posr].push_back(posl - 1);
bucket[posl - 1]++;
}
}
int main() {
ios::sync_with_stdio(false);
cin.tie(nullptr), cout.tie(nullptr);
cin >> q1 >> q2;
for(int j = 1; j <= q1; ++j) {
int l;
cin >> l;
for(int i = 1; i <= l; ++i) {
cin >> str[++n]; pos[n] = j;
}
str[++n] = 10000 + (++D);
cin >> l;
for(int i = 1; i <= l; ++i) {
cin >> str[++n]; pos[n] = j;
}
str[++n] = 10000 + (++D);
}
for(int j = q1 + 1; j <= q1 + q2; ++j) {
int l;
cin >> l; Len[j] = l;
for(int i = 1; i <= l; ++i) {
cin >> str[++n]; pos[n] = j;
}
lst[j] = n;
str[++n] = 10000 + (++D);
}
suffixArray();
lg2[0] = -1;
for(int i = 1; i <= n; ++i) {
lg2[i] = lg2[i / 2] + 1;
}
for(int i = 1; i <= n; ++i) {
st[i][0] = height[i];
}
for(int j = 1; (1 << j) <= n; ++j) {
for(int i = 1; i + (1 << j) - 1 <= n; ++i) {
st[i][j] = min(st[i][j - 1], st[i + (1 << (j - 1))][j - 1]);
}
}
for(int i = 1; i <= n; ++i) {
if(pos[sa[i]] <= q1 || lst[pos[sa[i]]] - sa[i] + 1 < Len[pos[sa[i]]]) continue;
work(i, Len[pos[sa[i]]]);
}
for(int i = 1; i <= n; ++i) {
if(appear[pos[sa[i]]] != 0) pre[i] = appear[pos[sa[i]]];
appear[pos[sa[i]]] = i;
}
for(int i = 1; i <= n; ++i) {
if(pos[sa[i]] <= q1) {
upd(pre[i] + 1, +1);
upd(i + 1, -1);
}
for(auto p: qu[i]) {
ans[p.second] = que(p.first);
}
}
memset(c, 0, sizeof c);
for(int i = 1; i <= n; ++i) {
upd(i, bucket[i]);
for(int p: adj[i]) {
upd(p, -1);
}
if(pos[sa[i]] <= q1) {
ans[pos[sa[i]]] += que(i) - que(pre[i]);
}
}
for(int i = q1 + 1; i <= q1 + q2; ++i) {
cout << ans[i] << '\n';
}
for(int i = 1; i <= q1; ++i) {
cout << ans[i] << ' ';
}
cout << '\n';
cout.flush();
return 0;
}
P4770 [NOI2018] 你的名字
给定串 $S$,每次询问 $[l,r]$ 和一个串 $T$,问 $T$ 的本质不同的子串有多少个不能匹配 $S[l\sim r]$ 的一部分。
考虑第一手容斥,转化为求 $T$ 的本质不同的子串有多少个能完全匹配 $S[l\sim r]$ 的一部分。
那么我们可以对于每个询问串后缀,求出 $p_i$ 代表当前询问串 $suf(i)$ 能够匹配 $S[l\sim r]$ 的最长长度。
本题中 $p$ 存在 $p_{rk_i}\geq p_{rk_{i-1}}-1$ 的性质(证明略),那么我们可以同样按照 $rk$ 从小到大求能以 $\mathcal{O}(|T|)$ 的速度找到 $p$,然后我们需要考虑如何进行检查是否合法。
我们记当前所做的 $p_i$ 对应的询问串的后缀为 $A$,那么相当于我们要找到 $S$ 的后缀 $B$,使得 $\text{lcp}(A,B)=|A|$ 且 $B$ 的首字母位置在 $S$ 的 $[l,r-p_i+1]$ 区间中。
首先我们可以通过倍增的方式找到区间 $[posl,posr]$ 使得它们的最长公共前缀为 $|A|$,而每一个位置相当于对应一个 $sa_i$ 的权值,代表这个后缀的开始位置,也就是说,我们用区间查询 $[posl,posr]$ 看里面是否存在 $i\in [posl,posr],\text{ s.t. }sa_i\in[l,r-p_i+1]$,这个东西我们直接上主席树维护,那么如果找到,说明 $p_i$ 长度仍可以变大,然后依次判断所有的即可。
注意最后找到所有 $p_i$ 后,答案的贡献与本质不同子串的计算不要重叠,具体可参考代码上实现。
时间复杂度 $\mathcal{O}(n\log n)$,空间复杂度 $\mathcal{O}(n\log n)$,代码常数较大。
代码
#include <bits/stdc++.h>
using namespace std;
typedef long long ll;
int n, m, q;
int str[1600005], be[100005], ed[100005];
char Tmp[1000005];
int L[100005], R[100005];
int pos[1600005];
int nxt[1600005], head[100005], Val[1600005];
int appear[1600005];
int lstl, lstr;
int st[1600005][21];
inline int lg2(int x) {
return 31 - __builtin_clz(x);
}
int query(int l, int r) {
int j = lg2(r - l + 1);
return min(st[l][j], st[r - (1 << j) + 1][j]);
}
int sa[1600005], rk[3200005], height[1600005];
int id[1600005], cnt[1600005], px[1600005], oldrk[3200005];
inline bool cmp(int x, int y, int j) {
return (oldrk[x] == oldrk[y] && oldrk[x + j] == oldrk[y + j]);
}
void suffixArray() {
m = max(n, 300 + q);
int i, j, t;
for(i = 1; i <= n; ++i) ++cnt[rk[i] = str[i]];
for(i = 1; i <= m; ++i) cnt[i] += cnt[i - 1];
for(i = n; i >= 1; --i) sa[cnt[rk[i]]--] = i;
for(j = 1; j < n; j <<= 1, m = t) {
for(t = 0, i = n; i > n - j; --i) id[++t] = i;
for(i = 1; i <= n; ++i)
if(sa[i] > j) id[++t] = sa[i] - j;
memset(cnt, 0, sizeof cnt);
for(i = 1; i <= n; ++i) ++cnt[px[i] = rk[id[i]]];
for(i = 1; i <= m; ++i) cnt[i] += cnt[i - 1];
for(i = n; i >= 1; --i) sa[cnt[px[i]]--] = id[i];
memcpy(oldrk, rk, sizeof oldrk);
for(t = 0, i = 1; i <= n; ++i)
rk[sa[i]] = cmp(sa[i], sa[i - 1], j) ? t : ++t;
if(t == n) break;
}
for(i = 1; i <= n; ++i) {
j = sa[rk[i] - 1];
int k = max(0, height[rk[i - 1]] - 1);
while(str[i + k] == str[j + k]) ++k;
height[rk[i]] = k;
}
}
int rt[1600005], node;
struct SegMent {
int l, r, cnt;
}tree[20000005];
inline int ls(int p) {return tree[p].l;}
inline int rs(int p) {return tree[p].r;}
void pushup(int p) {
tree[p].cnt = tree[ls(p)].cnt + tree[rs(p)].cnt;
}
int clone(int p) {
int q = ++node;
tree[q] = tree[p];
return q;
}
int ins(int p, int l, int r, int x) {
p = clone(p);
if(l == r) {
tree[p].cnt++;
}
else {
int mid = (l + r) >> 1;
if(x <= mid) {
tree[p].l = ins(ls(p), l, mid, x);
}
else {
tree[p].r = ins(rs(p), mid + 1, r, x);
}
pushup(p);
}
return p;
}
bool que(int p1, int p2, int l, int r, int ql, int qr) {
if(l == ql && r == qr) {
return tree[p2].cnt - tree[p1].cnt > 0;
}
int mid = (l + r) >> 1;
if(mid >= qr) {
return que(ls(p1), ls(p2), l, mid, ql, qr);
}
else if(mid + 1 <= ql) {
return que(rs(p1), rs(p2), mid + 1, r, ql, qr);
}
else {
return (que(ls(p1), ls(p2), l, mid, ql, mid) | que(rs(p1), rs(p2), mid + 1, r, mid + 1, qr));
}
}
bool chk(int p, int l, int ql, int qr) {
int posl = p, posr = p + 1;
if(height[p] >= l) {
for(int j = lg2(p - lstl + 1); j >= 0; --j) {
if(posl - (1 << j) >= 2 && st[posl - (1 << j)][j] >= l) {
posl -= (1 << j);
}
}
}
else {
posl = p + 1;
}
if(height[p + 1] >= l) {
for(int j = lg2(lstr - p + 1); j >= 0; --j) {
if(posr + (1 << j) - 1 <= n && st[posr][j] >= l) {
posr += (1 << j);
}
}
}
if(posl > posr) return false;
return que(rt[posl - 2], rt[posr - 1], 1, n, ql, qr);
}
int main() {
ios::sync_with_stdio(false);
cin.tie(nullptr), cout.tie(nullptr);
cin >> (Tmp + 1);
for(int i = 1, l = strlen(Tmp + 1); i <= l; ++i) {
str[++n] = Tmp[i];
}
str[++n] = 300;
cin >> q;
for(int j = 1; j <= q; ++j) {
cin >> (Tmp + 1) >> L[j] >> R[j];
be[j] = n + 1;
for(int i = 1, l = strlen(Tmp + 1); i <= l; ++i) {
str[++n] = Tmp[i]; pos[n] = j;
}
ed[j] = n;
str[++n] = 300 + j;
}
suffixArray();
for(int i = 1; i <= n; ++i) {
st[i][0] = height[i];
}
for(int j = 1; (1 << j) <= n; ++j) {
for(int i = 1; i + (1 << j) - 1 <= n; ++i) {
st[i][j] = min(st[i][j - 1], st[i + (1 << (j - 1))][j - 1]);
}
}
for(int i = 1; i <= n; ++i) {
if(str[sa[i]] > 'z' || pos[sa[i]] >= 1) rt[i] = rt[i - 1];
else rt[i] = ins(rt[i - 1], 1, n, sa[i]);
}
for(int i = 1; i <= n; ++i) {
if(head[pos[sa[i]]] != 0) {
nxt[i] = head[pos[sa[i]]];
}
head[pos[sa[i]]] = i;
}
for(int j = 1; j <= q; ++j) {
ll sum = 0, pp = 0;
for(int i = head[j]; i; i = nxt[i]) {
sum += ed[j] - sa[i] + 1;
if(nxt[i] != 0) Val[i] = query(nxt[i] + 1, i), sum -= Val[i];
else pp = i;
}
for(int i = be[j], k = 0; i <= ed[j]; ++i) {
k = max(0, k - 1);
lstl = 2, lstr = n;
while(i + k <= ed[j] && L[j] + k <= R[j] && chk(rk[i], k + 1, L[j], R[j] - k) == true) ++k; // 按顺序求 p[rk[i]] 的过程
if(rk[i] != pp) sum -= max(0, k - Val[rk[i]]);
else sum -= k;
}
cout << sum << '\n';
}
cout.flush();
return 0;
}
总结
- SA 的求解思路为倍增求长度为 $2^k$ 子串的字典序。
- 求 SA 复杂度 $\mathcal{O}(n\log n)$ ,一般作为整体代码瓶颈。
- 求 $\text{Height}$ 复杂度 $\mathcal{O}(n)$,注意式子 $height_{rk_i}\geq height_{rk_{i-1}}-1$ 的具体意义,和一些题目上的拓展应用(P4770 中 $p_{rk_i}\geq p_{rk_{i-1}}-1$ 就有类似性质)
- 求 $\text{lcp}$ 复杂度 $\mathcal{O}(n\log n)-\mathcal{O}(1)$
- 注意 $\text{lcp}$ 是区间最小值 $\text{Height}$ 的应用。(如用 $height_i\geq k$ 条件二分分组,离线涨水,或者 $\sum\text{lcp}(suf(i),suf(j))\Rightarrow \min\limits_{rk_i<k\leq rk_j}height_k$ 等等)
- 将 SA 问题转化为区间维护询问问题(CF204E 可转化为单调队列维护区间最大值,P2336 可转化为“HH的项链”经典区间维护问题)
参考致谢
- 教练的 ppt
- xMinh 的博客
- Crabby-Maskiv 的博客,学长 Orz
- 机巧人偶珂愛
- …
后续
话说 SAM 啥时候更。。
活过省选再说。