点分治
点分治,是一种基于树上的分治算法。
对于一棵树的贡献,拆成如下两部分:
- 各个子树的贡献
- 经过根节点路径的贡献
基于此,每次都选树的重心计算,由重心性质,最多递归 $O(\log n)$ 次即可到达叶子,则总共遍历节点的数量不超过 $O(n\log n)$,再套用一些数据结构解决路径的贡献,可以将复杂度做到 polylog。
我们基于一道例题来了解点分治的过程。
例题:P4149 [IOI2011]Race
给定一棵树,求一条路径,边权和为 $k$,且边的数量最少。
$n\le 2\times10^5,k\le 10^6$
我们构造一组样例,来帮助理解点分治的过程。
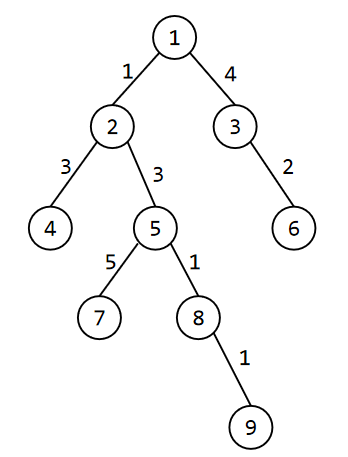
其中 $k=6$。
首先我们找到原树的重心,不难发现是 $2$。
那么我们以 $2$ 为根节点,先去求经过 $2$ 的路径为 $k$ 的最小值,一共有如下路径:
- $4-2-5$,边数为 $2$
- $1-2-5-8-9$,边数为 $4$
然后我们删除掉 $2$ 号点,每一棵子树都是一个子问题:
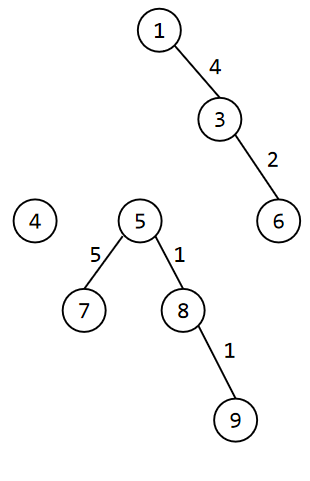
对于 $①③⑥$ 子树,$3$ 号是这棵树的重心,计算经过 $3$ 号点的且边权和为 $k$ 的路径:
- $1-3-6$,边数为 $2$
然后删除 $3$ 号点,将其分为两个 $1$ 个节点形成的树,没有贡献,故不再叙述。
对于这个 $⑤⑦⑧⑨$ 子树,选 $5$ 作为树的重心,计算经过 $5$ 号点的且边权和为 $k$ 的路径:
- $7-5-8$,边数为 $2$
然后删除 $5$ 号点,分开后的 $2$ 棵子树都没有边权和为 $k$ 的路径,不再叙述。
对于 $④$ 子树,没有贡献。
综上,答案为 $2$。
代码实现
理解了过程,接下来详细地说一说代码实现和一些细节。
1. 初始化-建树
这里指的建树只是将输入的边存储起来。
const int maxn = 200005;
int n, k, top, head[maxn];
struct Edge {
int v;
int w;
int next;
}Edge[2 * maxn];
void insert(int u, int v, int w) {
Edge[++top].v = v;
Edge[top].w = w;
Edge[top].next = head[u];
head[u] = top;
}
scanf("%d%d", &n, &k);
for(int i = 1;i <= n - 1;i++) {
int u, v, w;
scanf("%d%d%d", &u, &v, &w);
u++, v++;
insert(u, v, w), insert(v, u, w);
}
2. 寻找重心
我们要对于当前的树找到重心,为了不跳到其它的子树上,用 $vis$ 数组记录已经使用的节点。
int node, res;
// sz: 子树大小(用于计算重心)
void dfs_node(int m, int u, int fa) {
sz[u] = 1;
int ma = -1;
for(int i = head[u];i;i = Edge[i].next) {
int v = Edge[i].v;
if(vis[v] == true || v == fa) continue;
dfs_node(m, v, u);
sz[u] += sz[v];
ma = max(ma, sz[v]);
}
ma = max(ma, m - sz[u]);
if(res > ma) {
res = ma, node = u;
}
}
3. 计算以当前根节点的贡献
注意到 $k\le 10^6$,也就是大于 $10^6$ 时一定没有贡献,我们用桶来记录某个长度的路径的最少边数,对于当前的子树,考虑之前加进桶里的答案与当前子树的合并,具体见代码。
// ww: 新树的子树大小(之前的 sz 用于求出重心,选出重心后,子树的大小会发生变化,我们要用新的子树大小求子树的重心)
// dis: 重心到此节点的距离
// dep: 此节点相对重心的深度,用于计算路径长度
// bucket: 用于存放最优解的桶
void dfs_sz(int u, int fa, int lstw) {
ww[u] = 1, dis[u] = dis[fa] + lstw, dep[u] = dep[fa] + 1;
for(int i = head[u];i;i = Edge[i].next) {
int v = Edge[i].v, w = Edge[i].w;
if(vis[v] == true || v == fa) continue;
dfs_sz(v, u, w);
ww[u] += ww[v];
}
if(dis[u] <= k) {
if(bucket[k - dis[u]] != Inf) {
ans = min((ll)ans, bucket[k - dis[u]] + dep[u]);
}
seq1[++cnt] = dis[u], seq2[cnt] = dep[u]; // 将本棵子树的信息存储,一会加入到桶数组中
}
}
4. 点分治
将上述代码加入至点分治的过程中,并继续递归,不要忘了清空数组。
void dfs(int m, int u) { // m: 当且子树的大小
res = Inf;
dfs_node(m, u, 0);
u = node, vis[u] = true;
dis[u] = 0, dep[u] = 0, cnt = 0;
bucket[dis[u]] = dep[u];
int lst = 0;
for(int i = head[u];i;i = Edge[i].next) {
int v = Edge[i].v, w = Edge[i].w;
if(vis[v] == true) continue;
dfs_sz(v, u, w);
ww[u] += ww[v];
for(int j = lst + 1;j <= cnt;j++) { // 将刚刚遍历的子树的信息放入桶中
bucket[seq1[j]] = min(bucket[seq1[j]], seq2[j]);
}
lst = cnt;
}
for(int i = 1;i <= cnt;i++) { // 按需清空 bucket
bucket[seq1[i]] = Inf;
}
for(int i = head[u];i;i = Edge[i].next) { // 递归求解
int v = Edge[i].v;
if(vis[v] == true) continue;
dfs(ww[v], v);
}
}
以上就是本题的绝大部分的内容,请读者结合代码理解。
动态点分治
动态点分治,就是在询问的基础上增加修改,如果修改一次,重新做一次点分治,复杂度太高,有没有一些快速维护的办法?
我们来思考点分治的过程:对于一个子树,找到其中心,其它点都对此点尝试去做贡献。
基于此点,我们引入一个概念。
点分树
每次点分治的过程中,将当前子树的重心与上一次子树的重心连边所形成的图称为点分树。
点分树的一个重要性质:是一个高度不超过 $\log n$ 的树,所有点的总深度不超过 $n\times \log n=n\log n$。
但由于这样会改变树的形态,所以只能维护一些不需要树的具体形态的问题。
所以动态点分治的过程大概就是:
- 跑一遍点分治,记录点分树,一些信息要在原有的树上进行计算
- 修改时在点分树上暴力跳祖先,并修改答案
- 询问直接输答案
习题
P3806【模板】点分治1
板子题,用来练练手,将路径的权值开桶,可以将复杂度做到 $O(nm\log n)$。
代码
#include <bits/stdc++.h>
using namespace std;
typedef long long ll;
const int maxn = 10005;
const int Inf = 0x3f3f3f3f;
int n, m, top, head[maxn];
int sz[maxn], ww[maxn], dis[maxn];
int q[105], ans[105];
bool vis[maxn];
int seq[maxn], cnt;
bool bucket[10000005];
struct Edge {
int v;
int w;
int next;
}Edge[2 * maxn];
void insert(int u, int v, int w) {
Edge[++top].v = v;
Edge[top].w = w;
Edge[top].next = head[u];
head[u] = top;
}
int node, res;
void dfs_sz(int rt, int u, int fa, int lstw) {
ww[u] = 1, dis[u] = dis[fa] + lstw;
for(int i = head[u];i;i = Edge[i].next) {
int v = Edge[i].v, w = Edge[i].w;
if(vis[v] == true || v == fa) continue;
dfs_sz(rt, v, u, w);
ww[u] += ww[v];
}
if(dis[u] <= 10000000) {
for(int i = 1;i <= m;i++) {
if(q[i] - dis[u] >= 0 && bucket[q[i] - dis[u]] == true) {
ans[i] = true;
}
}
++cnt, seq[cnt] = dis[u];
}
}
void dfs_node(int m, int u, int fa) {
sz[u] = 1;
int ma = -1;
for(int i = head[u];i;i = Edge[i].next) {
int v = Edge[i].v;
if(vis[v] == true || v == fa) continue;
dfs_node(m, v, u);
sz[u] += sz[v];
ma = max(ma, sz[v]);
}
ma = max(ma, m - sz[u]);
if(ma < res) {
res = ma, node = u;
}
}
void dfs(int m, int u) {
res = Inf;
dfs_node(m, u, 0);
u = node, vis[u] = true, cnt = 0;
dis[u] = 0;
bucket[dis[u]] = true;
cnt = 0;
int lst = 0;
for(int i = head[u];i;i = Edge[i].next) {
int v = Edge[i].v, w = Edge[i].w;
if(vis[v] == true) continue;
dfs_sz(v, v, u, w);
ww[u] += ww[v];
for(int i = lst + 1;i <= cnt;i++) {
bucket[seq[i]] = true;
}
lst = cnt;
}
for(int i = 1;i <= cnt;i++) {
bucket[seq[i]] = false;
}
bucket[dis[u]] = false;
for(int i = head[u];i;i = Edge[i].next) {
int v = Edge[i].v;
if(vis[v] == true) continue;
dfs(ww[v], v);
}
}
int main() {
scanf("%d%d", &n, &m);
for(int i = 1;i <= n - 1;i++) {
int u, v, w;
scanf("%d%d%d", &u, &v, &w);
insert(u, v, w);
insert(v, u, w);
}
for(int i = 1;i <= m;i++) {
scanf("%d", &q[i]);
}
dfs(n, 1);
for(int i = 1;i <= m;i++) {
if(ans[i] == true) puts("AYE");
else puts("NAY");
}
return 0;
}
P2634 [国家集训队]聪聪可可
继续练手,完全没难度。
P2056 [ZJOI2007] 捉迷藏
这题还是有点意思,一道动态点分治,只需考虑修改时去如何维护。
考虑点分治时是如何去计算答案,对于一个以 $u$ 为根的子树,实际上就是找到 $u$ 的子树中最深的根节点和之前 $u$ 的其它子树的关节点合并。
所与对于一个以 $u$,我们要干两件事情:
- 找到两个最深的关节点,更新全局答案
- 上传一个此棵子树最深的关节点,方便父节点的计算
那么我们可以用堆维护这些信息。一个记录当前节点 $u$ 的每个子树内的一个最深的关节点,再用一个堆记录当前 $u$ 节点中所有关节点到 $u$ 节点的父亲 $fa$ 的距离。然后再用堆去进行删除标记。
注意一点:距离信息一定要在原树上统计!距离信息一定要在原树上统计!距离信息一定要在原树上统计!
代码
#include <bits/stdc++.h>
using namespace std;
const int maxn = 100005;
const int Inf = 0x3f3f3f3f;
int read() {
int res = 0, ch = getchar();
while(!(ch >= '0' && ch <= '9') && ch != EOF) {
ch = getchar();
}
while(ch >= '0' && ch <= '9') {
res = (res << 3) + (res << 1) + (ch - '0');
ch = getchar();
}
return res;
}
int readop() {
int ch = getchar();
while(!(ch == 'G' || ch == 'C') && ch != EOF) {
ch = getchar();
}
if(ch == 'G') {
return 0;
}
else {
return 1;
}
}
void write(int x) {
if(x < 0) {
putchar('-');
x = -x;
}
if(x > 9) {
write(x / 10);
}
putchar(x % 10 + '0');
}
int n, q, top, head[maxn];
int p[maxn], sz[maxn], ww[maxn], cur[maxn];
int dist[maxn][20], dep[maxn];
bool vis[maxn], state[maxn];
struct Edge {
int v;
int next;
}Edge[2 * maxn];
void insert(int u, int v) {
Edge[++top].v = v;
Edge[top].next = head[u];
head[u] = top;
}
struct Heap {
priority_queue<int> q, del;
inline int fima() {
while(!q.empty() && !del.empty()) {
if(q.top() == del.top()) {
q.pop(), del.pop();
}
else {
return q.top();
}
}
if(!q.empty()) return q.top();
else return -Inf;
}
inline int sema() {
int x = fima();
if(x == -Inf) return x;
q.pop();
int y = fima();
q.push(x);
return y;
}
inline void pu(int x) {
q.push(x);
}
inline void remove(int x) {
del.push(x);
}
}globe, fadis[maxn], madis[maxn];
int res, node;
void dfs_node(int m, int u, int fa) {
sz[u] = 1;
int ma = -1;
for(int i = head[u];i;i = Edge[i].next) {
int v = Edge[i].v;
if(vis[v] == true || v == fa) continue;
dfs_node(m, v, u);
sz[u] += sz[v];
ma = max(ma, sz[v]);
}
ma = max(ma, m - sz[u]);
if(res > ma) {
res = ma, node = u;
}
}
void dfs_sz(int u, int fa) {
ww[u] = 1;
for(int i = head[u];i;i = Edge[i].next) {
int v = Edge[i].v;
if(vis[v] == true || v == fa) continue;
dfs_sz(v, u);
ww[u] += ww[v];
}
}
int seq[maxn], cnt;
void bfs(int st, int nowdep) {
queue<int> q;
q.push(st), q.push(0);
while(!q.empty()) {
int u = q.front();q.pop();
seq[++cnt] = u;
int fa = q.front();q.pop();
dist[u][nowdep] = dist[fa][nowdep] + 1;
for(int i = head[u];i;i = Edge[i].next) {
int v = Edge[i].v;
if(vis[v] == true || v == fa) continue;
q.push(v), q.push(u);
}
}
}
void dfs_build(int m, int u, int fa, int nowdep) {
cnt = 0;
bfs(u, nowdep);
res = Inf;
dfs_node(m, u, 0);
u = node, vis[u] = true;
for(int i = 1;i <= cnt;i++) {
fadis[u].pu(dist[seq[i]][nowdep]);
}
p[u] = fa;
dep[u] = dep[fa] + 1;
dfs_sz(u, 0);
for(int i = head[u];i;i = Edge[i].next) {
int v = Edge[i].v;
if(vis[v] == true || v == fa) continue;
dfs_build(ww[v], v, u, nowdep + 1);
}
if(fa != 0) {
madis[fa].pu(fadis[u].fima());
}
madis[u].pu(0), cur[u] = madis[u].fima() + madis[u].sema();
globe.pu(cur[u]);
}
int main() {
n = read();
for(int i = 1;i <= n - 1;i++) {
int u = read(), v = read();
insert(u, v);
insert(v, u);
}
dfs_build(n, 1, 0, 1);
int tot = n;
q = read();
while(q--) {
int op = readop(), x;
if(op == 0) {
if(tot == 0) write(-1), putchar('\n');
else if(tot == 1) write(0), putchar('\n');
else write(globe.fima()), putchar('\n');
}
else {
x = read();
if(state[x] == true) madis[x].pu(0), tot++;
else madis[x].remove(0), tot--;
int u = x, res;
while(true) {
res = madis[u].fima() + madis[u].sema();
if(res != cur[u]) {
globe.remove(cur[u]);
cur[u] = res;
globe.pu(cur[u]);
}
if(p[u] == 0) break;
res = fadis[u].fima();
if(state[x] == true) fadis[u].pu(dist[x][dep[u]]);
else fadis[u].remove(dist[x][dep[u]]);
int res0 = fadis[u].fima();
if(res != res0) {
madis[p[u]].remove(res);
madis[p[u]].pu(res0);
}
u = p[u];
}
state[x] ^= 1;
}
}
return 0;
}
P4292 [WC2010]重建计划
这题是真的恶心,可以合理质疑现在大部分题解都存在一定的卡精问题。
首先看到平均值最大,不难先想到二分一手,将每条边都减去 $mid$,然后只需选出 $1$ 条符合长度要求的路径,边权和不小于 $0$ 即可。
对于当前正在解决的树,考虑记 $bucket_i$ 表示之前子树中相对深度节点为 $i$ 的最大边权和,$tmp_i$ 表示当前子树中相对深度节点为 $i$ 的最大边权和。
特别地,记 $bucket_0=0$。
在将 $tmp$ 合并入 $bucket$ 前,我们要先判断当前的两部分是否能拼成大于 $0$ 的路径。
我们这里记 $u$ 子树的最深深度为 $z_u$,如果不用 $z_u$ 复杂度不对,当 $bucket$ 的深度取 $i$ 时,$tmp$ 的选取范围为 $[L-i,R-i]$,注意到当 $i$ 减小时,$tmp$ 的选取向右滑动,这样我们倒序枚举 $i$,用单调队列维护最大值。
如果从 $R-1$ 开始,复杂度就炸了,所以具体实现时,我们可以分为两部分。
- 当 $i\in [\max(R-z_u, 0),R-1]$,此时 $R-i\in[1,z_u]$,但 $i\in [0,z_u]$ 不一定成立。此时我们只需尝试插入队列,排除不合法的队头,并判断是否可以更新。
- 当 $i\in[0,min(z_u, max(R-z_u,0)-1)]$ 时,此时 $R-i\in[1,z_u]$ 不一定成立,但 $i\in[0,z_u]$ 一定成立,这时我们只需排除不合法的队头,并判断是否可以更新。
至于其它的部分,那都压根没用,这样复杂度就严格限制在了 $O(\sum z)=O(n\log n)$。
综上,本题的复杂度为 $O(n\log^2 n)$。
注意要先预处理关于重心和 $z$ 的信息,否则常数太大会被卡。
代码
#include <bits/stdc++.h>
using namespace std;
typedef long long ll;
typedef long double lf;
const int maxn = 100005;
int read() {
int res = 0, ch = getchar();
while(!(ch >= '0' && ch <= '9') && ch != EOF) {
ch = getchar();
}
while(ch >= '0' && ch <= '9') {
res = (res << 3) + (res << 1) + (ch - '0');
ch = getchar();
}
return res;
}
int n, top, head[maxn];
int L, R;
int sz[maxn], ww[maxn][25];
bool vis[maxn];
struct Edge {
int v;
ll w;
int next;
}Edge[2 * maxn];
void insert(int u, int v, ll w) {
Edge[++top].v = v;
Edge[top].w = w;
Edge[top].next = head[u];
head[u] = top;
}
int node[maxn][25], res;
void dfs_node(int m, int u, int fa, int rt, int g) {
sz[u] = 1;
int ma = -1;
for(int i = head[u];i;i = Edge[i].next) {
int v = Edge[i].v;
if(vis[v] == true || v == fa) continue;
dfs_node(m, v, u, rt, g);
sz[u] += sz[v];
ma = max(ma, sz[v]);
}
ma = max(ma, m - sz[u]);
if(res > ma) {
res = ma, node[rt][g] = u;
}
}
bool flag;
ll bucket[maxn], tmp[maxn];
ll mares;
void dfs_dis(int u, int fa, int dep, ll dis, ll k) {
tmp[dep] = max(tmp[dep], dis);
for(int i = head[u];i;i = Edge[i].next) {
ll v = Edge[i].v, w = Edge[i].w;
if(vis[v] == true || v == fa) continue;
dfs_dis(v, u, dep + 1, dis + w - k, k);
}
}
int q[maxn], h, t;
int z[maxn];
void dfs_ww(int u, int fa, int g, int dep, int rt) {
z[rt] = max(z[rt], dep);
ww[u][g] = 1;
for(int i = head[u];i;i = Edge[i].next) {
int v = Edge[i].v;
if(vis[v] == true || v == fa) continue;
dfs_ww(v, u, g, dep + 1, rt);
ww[u][g] += ww[v][g];
}
}
void merge(int u) {
h = 1, t = 0;
for(int i = R - 1;i >= max(R - z[u], 0);i--) {
while(h <= t && q[h] < L - i) {
h++;
}
while(h <= t && tmp[q[t]] < tmp[R - i]) {
t--;
}
q[++t] = R - i;
if(h <= t && i <= z[u]) {
mares = max(mares, bucket[i] + tmp[q[h]]);
if(bucket[i] + tmp[q[h]] >= 0) {
flag = true;
break;
}
}
}
for(int i = min(max(R - z[u], 0) - 1, z[u]);i >= 0;i--) {
while(h <= t && q[h] < L - i) {
h++;
}
if(h <= t && q[h] <= R - i) {
mares = max(mares, bucket[i] + tmp[q[h]]);
if(bucket[i] + tmp[q[h]] >= 0) {
flag = true;
break;
}
}
}
for(int i = 1;i <= z[u];i++) {
bucket[i] = max(bucket[i], tmp[i]);
}
}
bool dfs(int m, int u, ll k, int g) {
u = node[u][g];
vis[u] = true, flag = false;
for(int i = 0;i <= z[u];i++) {
bucket[i] = -1e18;
}
bucket[0] = 0;
for(int i = head[u];i;i = Edge[i].next) {
ll v = Edge[i].v, w = Edge[i].w;
if(vis[v] == true) continue;
for(int j = 1;j <= z[u];j++) {
tmp[j] = -1e18;
}
dfs_dis(v, 0, 1, w - k, k);
merge(u);
if(flag == true) {
return true;
}
}
for(int i = head[u];i;i = Edge[i].next) {
int v = Edge[i].v;
if(vis[v] == true) continue;
if(dfs(ww[v][g], v, k, g + 1) == true) return true;
}
return false;
}
bool check(ll k) {
for(int i = 1;i <= n;i++) {
vis[i] = false;
}
return dfs(n, 1, k, 0);
}
void build_tree(int m, int u, int fa, int g) {
res = 1e9;
dfs_node(m, u, 0, u, g);
u = node[u][g];
vis[u] = true;
dfs_ww(u, 0, g, 0, u);
for(int i = head[u];i;i = Edge[i].next) {
int v = Edge[i].v;
if(vis[v] == true || v == fa) continue;
build_tree(ww[v][g], v, u, g + 1);
}
}
int main() {
n = read();
L = read(), R = read();
for(int i = 1;i <= n - 1;i++) {
ll u = read(), v = read(), w = read();
insert(u, v, w * 10000);
insert(v, u, w * 10000);
}
build_tree(n, 1, 0, 0);
ll l = 1, r = 1e10, mid, ans = l;
while(l <= r) {
mid = (l + r) >> 1;
mares = -1e18;
if(check(mid) == true) {
l = mid + 1, ans = mid;
}
else {
r = mid - 1;
}
}
printf("%.3Lf\n", (lf)ans / 10000);
return 0;
}
总结
没啥要说的,有好题继续更新。