流网络 $\text{(Flow Network)}$
对于一个有向图 $G=(V,E)$,$\forall(u,v)\in E$,有一个权值 $c(u,v)$,代表 $u\rightarrow v$ 这条边的流量 $\text{(capacity)}$,当 $(u,v)\notin E$ 时有 $c(u,v)=0$。
在这个有向图中,存在 $s\in V,t\in V$,我们称之为源点 $\text{(source)}$ 和汇点 $\text{(sink)}$,且 $s\neq t$ 。
我们把这样的图称之为网络。
可行流 $\text{(Flow)}$
$\forall u\in V,v\in V$,定义函数 $f(u,v)$ 为 $u\rightarrow v$ 的流量,$c’(u,v)=c(u,v)-f(u,v)\ge 0$ 称为 $u\rightarrow v$ 的剩余容量。此时不考虑反向边会比较好。
我们定义可行流函数 $f(u,v)$ 满足如下性质:
- $\forall(u,v)\in E,f(u,v)\le c(u,v)$,任意一条边的流量不超过这条边的容量。
- $\forall x\in V,x\neq s,t,\sum\limits_{(u,x)\in E}f(u,x)=\sum\limits_{(x,v)\in E}f(x,v)$,即任意一个点,进入这个点的流量都等于出去的流量。
一个网络的流就是源点发出的全部流量,记 $F=\sum\limits_{\forall(s,u)\in E}f(s,u)$。
残留网络
残留网络的点集和边集与原网络是一样的,但唯一不同的是每条边存在一个剩余容量,这里我们对于一个有向边,考虑其的反向边:
- 当 $(u,v)\in E$,$c’(u,v)=c(u,v)-f(u,v),c’(v,u)=f(u,v)$。
反向边的加入是为了存在反悔贪心的操作,保证了算法正确性,在程序中我们所建的都是残留网络。
增广路
对于一条从 $s$ 到 $t$ 的路径,对于路径上任意一条边 $(u,v)$,满足 $c’(u,v)>0$,我们就称这条路径为增广路。
那么如果有了一条增广路,我们就会尝试让源点分一点流量给这条增广路,而分配的流量就是每条边剩余容量的最小值(显然多了也流不过去),不难发现,当网络中存在增广路,则最大流答案将变大。
割
如果有网络 $G=(V,E)$,存在集合 $S,T\subseteq V,S\cap T=\emptyset,S\cup T=V,s\in S,t\in T$,则称 $S,T$ 是对于网络 $G$ 的一个割。
割的容量
对于一个割 $S,T$,$c(S,T)=\sum\limits_{u\in S,v\in T,(u,v)\in E}c(u,v)$,我们称之为割的容量。
最小割
最小割的指的是割的最小容量。
割的流量
对于一个割 $S,T$,$f(S,T)=\sum\limits_{u\in S,v\in T, (u,v)\in E}f(u,v)-\sum\limits_{u\in S,v\in T,(u,v)\in E}f(v,u)$,我们称之为割的容量。
意思为从 $S$ 中的点流到 $T$ 中的点的流量减去从 $T$ 的点流回到 $S$ 的点的流量。
割的性质
$f(X,Y)+f(Y,X)=0$
$f(X,X)=0$
$f(Z,X\cup Y)=f(Z,X)+f(Z,Y)$
$f(X\cup Y,Z)=f(X,Z)+f(Y,Z)$
$\forall [S,T],\forall f,f(S,T)\le c(S,T)$。即任意的一个割与原网络的任意一个可行流,有割的流量不超过割的容量。
$f(S,T)=F$,即割的流量等于原网络的可行流。
证明:
$\because f(S,V)=f(S,S)+f(S,T)$(性质 $3$)且 $f(S,S)=0$(性质 $2$)
$\therefore f(S,V)=f(S,T)$
又 $\because f(S,V)=f({s},V)+f(S\backslash{s},V)$ (性质 $4$)
记 $S’=S\backslash {s}$,$S’$ 中不存在源点和汇点,则流量守恒,有 $f(S’,V)=0$
$\therefore f(S,T)=f({s},V)=F$
$F\le c(S,T)$,由性质 $5,6$ 可得。则我们能得到最大流不超过最小割。
最大流
对于一个在网络的所有可行流,所得到的最大的 $F$ 称为网络的最大流,记作 $F_{\max}$。
最大流指的是最大可行流。
*最大流最小割定理
最大流最小割定理指的是这样 $3$ 个条件互相等价:
$\text{A.}$ 原网络取到最大流 $F_{\max}$
$\text{B.}$ 残留网络中不存在增广路
$\text{C.}$ 存在 $[S,T],c(S,T)=F$
证明:
$\mathcal{I.}\text{A}\Rightarrow \text{B}$
若当原网络取到最大流 $F_{\max}$ 时,残留网络仍存在增广路。
那么我可以通过增广这条增广路的方式增加原网络流量使其不是最大流。
证毕。
$\mathcal{II.}\text{B}\Rightarrow\text{C}$
由于只需存在一个割满足,那么考虑一种构造方式:
对于当前的残留网络,$S$ 集合为源点 $s$ 通过剩余容量不为 $0$ 的边可到达的点集,$T$ 为 $V\backslash S$。
由于 $\text{B}$ 条件,所以 $S$ 集合一定不包含 $t$。
考虑此时的 $c(S,T)$。
$\forall u\in S,v\in T$,我们有 $f(u,v)=c(u,v)$。如果 $f(u,v)< c(u,v)$,那么在残留网络中这条边的剩余流量 $c’(u,v)=c(u,v)-f(u,v)>0$,则 $v$ 应该也在 $S$ 中矛盾。
$\forall u\in S, v\in T$,我们有 $f(v,u)=0$,证明方式同上。
那么我们有 $f(S,T)=\sum\limits_{u\in S,v\in T, (u,v)\in E}f(u,v)-\sum\limits_{u\in S,v\in T,(u,v)\in E}f(v,u)=\sum\limits_{u\in S,v\in T,(u,v)\in E}c(u,v)=c(S,T)$
又有 $f(S,T)=F$,$\therefore c(S,T)=F$,证毕。
$\mathcal{III.}\text{C}\Rightarrow A$
原命题 $\Leftrightarrow$ $F=c(S,T)=F_{\max}$
由性质 $7$,最大流小于等于最小割。
最小割 $\le c(S,T)=F\le F_{\max}$
所以最小割小于等于最大流,所以最小割等于最大流,同时得到 $F$ 就是最大流。
证毕。
那么我们就得到了,残留网络中没有增广路和当前的流是最大流是充要条件。
最大流算法
$\text{Edmonds Karp}$
网络最大流是怎么求的呢?有了对于增广路的概念,我们不难想到一个较为朴素的做法:在当前残留网络中,找到一条增广路,如果能找到增广路,说明当前的流的答案会变大,增加流,然后把增广路上的每条边的容量减掉增广路上所有边的最小容量,重复过程直到不能找到增广路。
乍一看十分之正确,但是存在一个问题:对于这样的一个贪心模拟的过程是否存在着后效性?
答案是有可能的,比如有 $s\rightarrow 1\rightarrow 2\rightarrow t,s\rightarrow1\rightarrow3\rightarrow t,s\rightarrow3\rightarrow t$ 这 $3$ 条增广路,如果我们恰好先选了 $s\rightarrow1\rightarrow3\rightarrow t$ 这条,然后恰好增广后 $c’(3,t)$ 变为 $0$,那不就增广不到 $s\rightarrow3\rightarrow t$ 了,但是显然我们还有增广 $s\rightarrow 1\rightarrow 2\rightarrow t,s\rightarrow3\rightarrow t$ 这两条路径的选择,那怎么处理这种情况呢?
问题的本质是存在后效性,那么能不能想办法采用类似反悔贪心的做法来做?
考虑为每条边开一个反向边。初始时反向边容量设为 $0$。
在我们增广了一次之后,将增广的路径上的正向边减少容量,反向边增加容量,这样上面的情况就会被反悔出来。
由于最大流最小割定理,所以只要残留网络中没有增广路,则一定得到最大流。
实现十分的容易,就是扫整张网络找增广路,并修改路径上的容量。
时间复杂度
理论证明的复杂度为 $\mathcal{O}(nm^2)$,但远远不能达到此上界,可处理 $n\le 10^4$ 的网络。
代码
#include <bits/stdc++.h>
using namespace std;
const int N = 1005, M = 20005, Inf = 0x3f3f3f3f;
int n, m, S, T;
int flow;
int head[N], e[M], f[M], nxt[M], top;
int que[N], incf[N], pre[N];
bool vis[N];
void add(int a, int b, int c) {
e[top] = b, f[top] = c, nxt[top] = head[a], head[a] = top++;
e[top] = a, f[top] = 0, nxt[top] = head[b], head[b] = top++;
}
bool bfs() {
int hh = 0, tt = 1;
memset(vis, false, sizeof vis);
memset(incf, 0, sizeof incf);
que[hh] = S, vis[S] = true, incf[S] = Inf;
while(hh != tt) {
int u = que[hh++];
for(int i = head[u]; ~i; i = nxt[i]) {
int v = e[i];
if(vis[v] == false && f[i] > 0) {
vis[v] = true;
pre[v] = i;
incf[v] = min(incf[u], f[i]);
que[tt++] = v;
}
}
}
return incf[T] > 0;
}
void EdmondsKarp() {
while(bfs() == true) {
int t = incf[T];
flow += t;
for(int u = T; u != S; u = e[pre[u] ^ 1]) {
f[pre[u]] -= t, f[pre[u] ^ 1] += t;
}
}
}
int main() {
ios::sync_with_stdio(false);
cin.tie(nullptr), cout.tie(nullptr);
cin >> n >> m >> S >> T;
memset(head, -1, sizeof head);
while(m--) {
int u, v, c;
cin >> u >> v >> c;
add(u, v, c);
}
EdmondsKarp();
cout << flow << '\n';
cout.flush();
return 0;
}
$\text{Dinic}$
$\text{Dinic}$ 的主要思想也是增广,但是不同于 EK 的每次增广一条路径,$\text{Dinic}$ 可以增广多条路径。
那么我们就要用 dfs() 找增广路了,但在找增广路前,首先需要用 bfs() 做一些准备工作,具体就是标注 $dis_u$ 表示 $s\rightarrow u$ 的最短路径长度,当然这里指的是增广路路径长度,要不然跑就不用跑那么多遍。
这样我们实际是给网络标了一个 DAG 序,使 dfs() 不会进入死循环,而其特有的回溯功能可使我们遍历到多条增广路。
那么算法流程是:先用 bfs() 分层,然后 dfs(u, Flow) 表示走到了 $u$ 点,从 $s\rightarrow u$ 的最小的一条边的容量是 $Flow$,每次我们找一个 $v$,使得 $dep_v=dep_u+1$,然后在途中就去更新正向边和反向边。
优化 $1$
一个剪枝,搜的时候记录当前点的流出量 $used$,显然当 $used=Flow$ 时,给到 $u$ 点的流都被用光了,就不用继续再从 $u$ 增广了,可以直接从 $u$ 退出回溯。
优化 $2$
一个剪枝,叫做当前弧优化。
当我们在枚举 $u$ 的出边时,我们是按我们链式前向星存边的顺序枚举一条出边 $(u,v)$,而此时我们还有 $x_1\rightarrow u,x_2\rightarrow u,\cdots$ 这样的边。
当 $x_1\rightarrow u$,跑 $u$ 所有的出边找增广路。
当 $x_2\rightarrow u$,跑 $u$ 所有的出边找增广路。
当 $x_3\rightarrow u$,跑 $u$ 所有的出边找增广路。
$\cdots$
每次都重新跑了所有出边,但由于 dfs() 的性质可能在前面被枚举到的出边容量已经增广完了。
所以记录 $cur_u$ 表示当前 $u$ 的出边在 $cur_u$ 之前被枚举到的已经增广完了,我们现在从 $cur_u$ 再增广就可以了。
十分有用的优化。
优化 $3$
对于一条边 $u\rightarrow v$,如果从 $v$ 开始搜索得到的流已经为 $0$,那么这轮搜索中以后再到达 $v$ 的流仍然为 $0$,直接在当前轮中把 $v$ 删掉,实现可以是 $dep_v=Inf$ 或其它。
时间复杂度
理论证明的复杂度为 $\mathcal{O}(n^2m)$,但远远不能达到此上界,可处理 $n\le 10^5$ 的网络。
代码
#include <bits/stdc++.h>
using namespace std;
const int N = 10005, M = 200005, Inf = 0x3f3f3f3f;
int n, m, S, T;
int flow;
int head[N], e[M], f[M], nxt[M], top;
int que[N], dep[N], cur[N];
void add(int a, int b, int c) {
e[top] = b, f[top] = c, nxt[top] = head[a], head[a] = top++;
e[top] = a, f[top] = 0, nxt[top] = head[b], head[b] = top++;
}
bool bfs() {
int hh = 0, tt = 1;
memcpy(cur, head, sizeof cur);
memset(dep, 0x3f, sizeof dep);
que[hh] = S, dep[S] = 0;
while(hh != tt) {
int u = que[hh++];
for(int i = head[u]; ~i; i = nxt[i]) {
int v = e[i];
if(dep[v] == Inf && f[i] > 0) {
dep[v] = dep[u] + 1;
que[tt++] = v;
}
}
}
return (dep[T] != Inf);
}
int dfs(int u, int flow) {
if(u == T) {
return flow;
}
int used = 0;
for(int i = cur[u]; ~i; i = nxt[i]) {
cur[u] = i;
int v = e[i];
if(dep[v] == dep[u] + 1 && f[i] > 0) {
int low = dfs(v, min(f[i], flow - used));
if(low > 0) {
used += low, f[i] -= low, f[i ^ 1] += low;
if(used == flow) break;
}
else {
dep[v] = Inf;
}
}
}
return used;
}
void Dinic() {
while(bfs() == true) {
flow += dfs(S, Inf);
}
}
int main() {
ios::sync_with_stdio(false);
cin.tie(nullptr), cout.tie(nullptr);
cin >> n >> m >> S >> T;
memset(head, -1, sizeof head);
while(m--) {
int u, v, c;
cin >> u >> v >> c;
add(u, v, c);
}
Dinic();
cout << flow << '\n';
cout.flush();
return 0;
}
最大流相关模型和例题
二分图匹配
二分图匹配一般指的是存在两个点集,点集内部没有边,点集之间有若干条边相连,一个匹配指的是从边集中选出一个子集,使得一个点至多出现在一条边中。
我们将其抽象成一个网络流模型,对于每一条边 $(u,v)$,我们在网络中连一条容量为 $1$ 的 $u\rightarrow v$ 的边,这样当这条边的流量为 $1$ 时,代表这条边被选择。
P2756 飞行员配对方案问题
最典型的二分图匹配,我们向源点和每一个外籍飞行员连一条容量为 $1$ 的边,英国飞行员连一条容量为 $1$ 的边,然后外籍飞行员和英国飞行员之间的匹配连一条容量为 $1$ 的边。
我们需要先证明原问题的每一个可行解 $s$,对应一个网络中的可行流 $f$。可行流的满足条件为容量限制和流量守恒。
对于一个可行解 $s$ ,一个可行解满足每个人至多在一条匹配边中,这些边的流量设为 $1$,而其余匹配边的流量设为 $0$,对于所有外国籍的点,流出流量最多为 $1$;对于所有英国籍的点,流入流量最多为 $1$。我们可以用源点出边的流量和汇点入边的流量补上使其符合流量守恒,所以一个可行解必定对应一个可行流。
对于一个可行流 $f$ ,为了符合题意,不妨先假设每条边的流量为 $0$ 或 $1$。
因为满足流量守恒,所以除了源点和汇点外,每个点的流入的流量和流出的流量相等,外国籍点流入流量和英国记流出流量均最多为 $1$,则每个人要么不匹配,要么至多在一组匹配中,所以一个可行流一定是一个可行解。
所以现在我们证明了每个可行解 $s$ 和整数流量的可行流一一对应,那么当我们证明了只要整数流量的最大流就是全局最大流的话,那么最大流就是全局最优解。
这个证明比较简单:因为 $\text{Dinic}$ 算法中只用到了整数变量,且得到最大流的充要条件是残留网络中不存在增广路,那么由于 $\text{Dinic}$ 跑完后没有了增广路,所以整数流量的最大流也是所有情况的最大流。
代码:https://www.luogu.com.cn/record/101009585
P3254 圆桌问题
在这道题中,区别仅仅在于从每个点的容量限制的不同,因为一个单位有 $r_i$ 个人,我们从汇点向每个单位连一条容量为 $r_i$ 的边,一个餐桌容纳 $c_i$ 个人,我们从每个餐桌向汇点连一条容量为 $c_i$ 的边,然后因为一个单位的人最多向每个桌子之间派 $1$ 个人,所以每个单位向每个桌子连一条容量为 $1$ 的边,这样不难证明,当网络满流时即是合法方案,所以跑最大流看是不是满流即可。
代码:https://www.luogu.com.cn/record/101009737
无源汇上下界可行流
给定一个无源点和汇点的网络,每条边要求的流量存在上下界,求这个网络是否存在可行流。
因为没有源点和汇点,所以一个可行流需要保证所有的点满足流量守恒。
如果本题在没有下界的情况下,在初始什么流量也没有的时候,所有点均满足流量守恒,但如果我们先给所有边流下界的流量,并不能保证所有点流量守恒,那么我们为了满足流量守恒,我们可以记录 $A_i$ 表示 $i$ 号点流入流量下界之和减流出流量下界之和,那么对于流入流量小于流出流量的点,可以将流出流量多的部分分到虚拟汇点上,同理流入流量多的点我们就流量分到虚拟源点,这样我们就强行维护了流量守恒,当然我们还需要对原网络的边的上界改为上界减下界,所以最终只要虚拟源点到虚拟汇点的最大流为满流,则就保证了原图的网络的边都可满足上下界,且流量守恒。下面我们证明新网络的正确性。
我们不妨设原图为 $G$,可行流为 $f$,新图为 $G’$,满流为 $f’$。
那么对于一个原图可行流 $f$,这个流在 $G$ 上满足容量限制和流量守恒,那么对于 $G’$ 上的每一个点的流量,我们形式化地表达:$\text{flow}(u)=\sum\limits_{(v,u)\in E}(f(v,u)-\lim(v, u))-\sum\limits_{(u,v)\in E}(f(u,v)-\lim(u,v))+f’(S,u)-f’(u,T)$。
什么意思?就是在原图中有的那些边的流量,我们在新图中将它们的流量设为流量减下界,那么在新图中新增的边为每个点到虚拟源点/虚拟汇点的边,那么 $f’(S,u)-f’(u,T)$ 应该为 $A_u$,而 $A_u$ 恰好就是流入流量下界之和减流出流量下界之和!则有:
$\text{flow}(u)=\sum\limits_{(v,u)\in E}(f(v,u)-\lim(v, u))-\sum\limits_{(u,v)\in E}(f(u,v)-\lim(u,v))+A_u$
$=\sum\limits_{(v,u)\in E}f(v,u)-\sum\limits_{(u,v)\in E}f(u,v)$
而由于 $f$ 是个可行流,所以最终相减的两部分是相等的,所以我们有 $\text{flow}(u)=0$,即流 $f’$ 流量守恒,是一个可行流。当然容量限制一般是一定满足的,所以有时候会省略证明。
对于一个新图可行流 $f’$,这个流在 $G’$ 上满足容量限制和流量守恒,证明也是一个思路,把每个点那些流到源点和汇点的那些流量在扔回到其它连接这个点的边上,就能证明流量守恒,但是我们还需要注意一个限制:原图中每条边的下限限制。
这当然也是十分好说的,对于图 $G’$ 的每条不连接虚拟源点/汇点的边,有 $0\leq f’(u,v)\leq c(u,v)-\lim(u,v)$,那么由于 $f’$ 是满流,所以肯定保证每条边都至少能分到 $\lim(u,v)$ 所以有 $\lim(u,v)\leq f’(u,v)+\lim(u,v)\leq c(u,v)$。
LOJ#115. 无源汇有上下界可行流
最终流程:求 $A_i\rightarrow$ 建新的残留网络 $\rightarrow$ 跑最大流 $\rightarrow$ 判是否是满流
struct NetWork {
int ver, limit, capacity, nxt; // 注意可能会需要多记一个 limit
void ins(int u, int v, int l, int w) {
ver = v, limit = l, capacity = w, nxt = head[u];
head[u] = top;
}
}Net[20805];
int main() {
ios::sync_with_stdio(false);
cin.tie(nullptr), cout.tie(nullptr);
cin >> n >> m;
s = 0, t = n + 1;
for(int i = 1;i <= m;i++) {
int u, v, l, w;
cin >> u >> v >> l >> w;
Net[++top].ins(u, v, l, w - l);
Net[++top].ins(v, u, l, 0);
A[u] -= l, A[v] += l; // 求 A[i]
}
for(int i = 1;i <= n;i++) {
if(A[i] > 0) { // 流入的下界流量之和大于流出的下界流量之和,建 s -> i 的边。
Net[++top].ins(s, i, 0, A[i]);
Net[++top].ins(i, s, 0, 0);
sum += A[i]; // 注意求一下满流大小。
}
else { // 反之建 i -> t 的边。
Net[++top].ins(i, t, 0, -A[i]);
Net[++top].ins(t, i, 0, 0);
}
}
Dinic();
if(Flow != sum) {
cout << "NO\n";
}
else {
cout << "YES\n";
for(int i = 2;i <= 2 * m;i += 2) { // 在输出原网络流的方案时,流量 = 新网络流量 + 边的流量下界。
cout << Net[i ^ 1].capacity + Net[i].limit << '\n';
}
}
cout.flush();
return 0;
}
有源汇上下界可行流
有了源点和汇点之后,说明有两个点的流量守恒就不用满足了,那么考虑怎么转化为无源汇上下界可行流。
这里一个比较巧妙的操作是连 $t\rightarrow s$ 并将容量设为 $\text{Inf}$,此时我们发现原图的源点和汇点也可以满足要求,然后我们按无源汇上下界可行流做就行。
有源汇上下界最小/大流
一个十分复杂的题目(指证明)
我们可以轻易的求一个可行流,但是如何找到最小或最大流呢,做法十分之简单:按有源汇上下界可行流跑虚拟源点到虚拟汇点的最大流,然后把 $t\rightarrow s$ 的边在残留网络中删掉,然后跑 $s$ 到 $t$ 的最大流,最终的最大流就是第一部分的最大流加第二部分的最大流,如果是最小流就跑 $t$ 到 $s$ 的最大流,最小流就是第一部分的最大流减第二部分的最大流。
下面我们来证明一下。
我们设原图为 $G$,原图的一个可行流为 $f$,我们设按有源汇上下界可行流建出来的图为 $G’$,一个满流为 $f’$,$G’$ 的残留网络记为 $G_{f’}$,残留网络的可行流为 $f_0$。
那么我们首先观察 $f_0+f’$ 的性质。不难发现,$f_0$ 中与虚拟源点和虚拟汇点相关的边的流量均为 $0$,因为 $f_0$ 是可行流,所以虚拟源点和虚拟汇点在源点和汇点分别是 $s$ 和 $t$ 的情况下,就变成了一个普通点,也是需要满足流量守恒的,而虚拟源点和虚拟汇点又分别都只能流出去流量和流进去流量,因此不可能再给它们流量,所以 $f_0+f’$ 仍然是一个满足容量限制的 $G’$ 的一个满流,且由 $f_0$ 我们可以得到,除了 $s$ 和 $t$ 外,其它点都是流量守恒的,而 $s$ 和 $t$ 通过 $G’$ 的 $t\rightarrow s$ 的反向边,也是可以满足流量守恒这一点的。因此,我们说,对于任意一个可行流 $f_0$,存在一个满流 $f’$,使得 $f_0+f’$ 是仍然是满流,这样就对应了原图 $G$ 的可行流 $f$。
那么接下来我们观察任意两个 $G’$ 的满流相减 $f’-f’’$。
考虑到两个满流都保证了虚拟源点流出的流量和虚拟汇点流入的流量是满的,那么相减之后这些有关虚拟源点和虚拟汇点的边的流量均变为了 $0$,这是后续证明正确的重点。
那么我们看这个是否对应一个残留网络的可行流 $f_0$ 呢,答案是对应的。因为两个可行流相减肯定还是可行流(但注意这个减完得到的还是虚拟源点到虚拟汇点的可行流),且虚拟源点和虚拟汇点的边的流量都减到了 $0$,所以除去虚拟源点和虚拟汇点这两个点后,网络仍满足流量守恒,这就足以说明有一个 $f_0$ 的可行流。
所以综上,我们证明了:残留网络 $G_{f’}$ 上的可行流 $f_0$ 加上新图 $G’$ 的满流 $f’$ 就等价于一个原图的可行流 $f$。所以才有了开头那个看似十分感性但正确的做法。
LOJ#116. 有源汇有上下界最大流
int main() {
ios::sync_with_stdio(false);
cin.tie(nullptr), cout.tie(nullptr);
cin >> n >> m >> s >> t;
S = 0, T = n + 1;
for(int i = 1;i <= m;i++) {
int u, v, l, w;
cin >> u >> v >> l >> w;
Net[++top].ins(u, v, w - l);
Net[++top].ins(v, u, 0);
A[u] -= l, A[v] += l;
}
for(int i = 1;i <= n;i++) {
if(A[i] > 0) {
Net[++top].ins(S, i, A[i]);
Net[++top].ins(i, S, 0);
sum += A[i];
}
else {
Net[++top].ins(i, T, -A[i]);
Net[++top].ins(T, i, 0);
}
}
Net[++top].ins(t, s, I);
Net[++top].ins(s, t, 0);
Dinic();
if(Flow < sum) {
cout << "please go home to sleep\n";
}
else {
int res = Net[top].capacity;
Net[top].capacity = Net[top - 1].capacity = 0;
S = s, T = t;
Flow = 0;
Dinic();
cout << res + Flow << '\n';
}
cout.flush();
return 0;
}
使用最大流作为判定的问题
POJ#2455. Secret Milking Machine
求最长道路的最小可能长度,不难想到二分答案 $mid$,然后将 $>mid$ 的边都删掉就是我们所有用的边。
将所有能用的边的流量设为 $1$,以 $1$ 为源点,$n$ 为汇点跑最大流,看最大流是否大于等于 $T$。
代码:http://poj.org/showsource?solution_id=23967440
P2754 [CTSC1999] 家园 / 星际转移问题
不难发现此题也有单调性,如果 $x$ 天满足,那么 $x+1$ 天也满足。
那么考虑如何判定,则我们需要将问题转化为一张流网络。本题采用了对每一天分层的思想建图,我们分几类边说明。
我们令地球编号为 $0$,月球编号为 $n+1$,其余太空站编号不变。定义 ${day,i}$ 表示第 $day$ 天的第 $i$ 个点。
- 由于全部的人一开始都在地球,我们连一条 $(S,0)$,容量为 $Inf$ 的边,代表人从地球出发。
- 由于每个人可在他当前的太空站停留到下一天且没有人数的限制,我们连一条 $({day,i},{day+1,i})$,容量为 $Inf$ 的边,表示停留的情况。
- 如果一些人在某一天已经到达了 $n+1$ 号点,代表已经到达了终点,我们连一条 $({day,n+1},T)$,容量为 $Inf$ 的边,表示已经到达终点。
- 最后是有关太空船的连边,对于每一天,我们需要计算出每个船昨天停靠的太空站 $u$ 与今天停靠的太空船 $v$,且太空站有人数限制 $h$,那么连 $({day-1,u},{day,v})$,容量为 $h$ 的边,代表太空船运输的情况。
这样我们就建好了整张图,可以发现这张图是与原问题等价的,那么我们每次往后加一天的边和点,跑最大流判断流量是否大于等于需要运输的人数 $k$,如果等于输出答案退出。
那么什么情况下无解?考虑如果有合法解当且仅当 $0$ 与 $n+1$ 连通,用并查集维护并判断一下就能知道。当然如果当天数足够大但也没有满足也可以说明无解。
代码:https://www.luogu.com.cn/record/101010280
拆点最大流问题
在前面的问题中,我们了解到如果某条边有限制,那么直接修改这条边的容量就行,那么点上有限制该怎么做呢。我们可以考虑将一个点拆为入点和出点,之间用对应容量的边连接。
P2891 [USACO07OPEN]Dining G
本题类似于一个二分图匹配,我们需要对每个奶牛各匹配两个物品,那么按之前的建图方式建图,源点向食品连边,食品向奶牛连边,奶牛向饮料连边,饮料向汇点连边就完成转化?
简单思考可知两者并不等价,因为没有限制一个奶牛只能拿一个食品和一个饮料,所以我们需要添加这个限制,我们将奶牛拆成两个点,一个连食品,一个连饮料,最终在这两个点之间连一条容量为 $1$ 的边,这样每个奶牛只能至多匹配一组,与原题意等价。
代码:https://www.luogu.com.cn/record/101026249
P2766 最长不下降子序列问题
首先我们设 $g_i$ 表示前 $i$ 个数选出的不下降子序列的最长题目,这是一个普及组动态规划,随便写过。
然后考虑如何去最多的数量。观察到对于一个长为 $s$ 的子序列 $p$,一定满足 $g_{p_i}=i$,所以当且仅当一条流网络上恰好经过一条 $g$ 值为 $1\sim s$ 的路径才合法,那么可以想到如下建图方式:如果有 $j<i,a_j\leq a_i,g_j+1=g_i$,那么连一条 $j\rightarrow i$ 的容量为 $1$ 的边,源点向所有 $g_i=1$ 的点连边,所有 $g_i=s$ 的点向汇点连边,又因为每个数最多取一次,作为一个对于点的限制考虑拆点,这样我们就构造出了一个与原问题等价的流网络,求出最大流就是可选择的序列数。
当能使用多次 $a_1$ 和 $a_n$ 时,也就是我们破除了选择 $a_1$ 和 $a_n$ 的限制,将源点到 $1$ 的入点,$1$ 的入点到 $1$ 的出点,$n$ 的出点到汇点,$n$ 的入点到 $n$ 的出点的容量修改为 $Inf$ 即可。
注意当 $s=1$ 时,修改为 $Inf$ 后可能会使最大流也变成 $Inf$,所以可以特判一下。
代码:https://www.luogu.com.cn/record/101026610
POJ#3498. March of the Penguins
我们分步骤将原问题转化为一个等价的流网络:
- 一开始有一些企鹅在某些浮冰上:将源点向这些浮冰连容量为企鹅数量的边。
- 每个浮冰的起跳次数有限制:相当于对每个点的限制,将其拆为入点和出点,并连一条容量为跳跃次数的边。
- 距离小于等于 $D$ 的浮冰可以到达:枚举任意两个浮冰,看距离是否小于等于 $D$,然后向浮冰的出点向下一块的浮冰的入点连一条容量为 $Inf$ 的边。
- 找出所有可以汇合的浮冰:我们可以枚举一个点作为汇点,跑最大流看是否等于企鹅数量。
代码:http://poj.org/showsource?solution_id=23967744
最大流建图实战
SP4063 MPIGS - Sell Pigs
我们考虑如果某个猪舍从未被打开过,那么第一个打开这个猪舍的顾客相当于有了第一次的购买权,而后打开的顾客可理解为是在买前几次顾客买剩下的猪。由于前几个顾客购买后拥有调整猪舍的权利,打开的猪舍相当于也可能会被新顾客购买,尽管新顾客可能不能打开某个猪圈。
这提示我们采用一种建图方式体现顾客之间的购买和调整的先后顺序。
因此我们按如下方式建边:
- 如果某个顾客第一次打开一个猪舍,源点 $S$ 向这个猪舍连容量为此猪舍猪的数量大小的边。
- 如果某个顾客不是第一次打开一个猪舍,那么让上一个打开这个猪舍的顾客向这个顾客连边,容量为 $Inf$。
- 每个顾客向汇点 $T$ 连容量为顾客需求猪的数量大小的边。
这样的思路正确性在于:保证了每个顾客在购买时打开的猪圈一定是在上一次顾客购买之后的,上一次顾客购买后的调整就相当于是顾客之间的连边。
最后我们跑最大流即为答案。
代码:https://www.luogu.com.cn/record/101030821
最小割算法
$\text{Dinic}$
由于最小割等于最大流,所以我们直接使用 $\text{Dinic}$ 求最大流,就是这个网络的最小割。
顺便说明一个最小割构造方式,由最大流最小割定理的证明过程,当我们求出一个可行流后,沿着所有剩余容量大于 $0$ 的点一直走到的所有点放到 $S$ 集合,其余放到 $T$ 集合,那么 $[S,T]$ 就是一个与当前可行流相等的割的容量。
代码略。
最小割相关模型和例题
最小割直接应用
AcWing2279. 网络战争
对于平均最小边权,不难想到 01 分数规划的做法。
二分一个值 $mid$ 并判断是否可行,等价于判断 $\dfrac{\sum\limits_{e\in C}w_e}{|C|}\leq mid$。
移项后得 $\sum\limits_{e\in C}(w_e - mid)\leq 0$,由于本题中对于边割集的定义为删去这些边后 $s$ 和 $t$ 不连通,因此我们先将 $w_e\le mid$ 的边都选上,那么剩下的边中都为正权,为了最小化代价,我们选最小割即可。
注意精度问题。
#include <bits/stdc++.h>
using namespace std;
typedef long double lf;
const int N = 105, M = 805, Inf = 0x3f3f3f3f;
const lf eps = 1e-4;
int n, m, S, T;
lf flow;
int head[N], e[M], w[M], nxt[M], top;
int que[N], dep[N], cur[N];
lf f[M];
void add(int a, int b, int c) {
e[top] = b, w[top] = c, nxt[top] = head[a], head[a] = top++;
e[top] = a, w[top] = c, nxt[top] = head[b], head[b] = top++;
}
bool bfs() {
int hh = 0, tt = 1;
memcpy(cur, head, sizeof cur);
memset(dep, 0x3f, sizeof dep);
que[hh] = S, dep[S] = 0;
while(hh != tt) {
int u = que[hh++];
for(int i = head[u]; ~i; i = nxt[i]) {
int v = e[i];
if(dep[v] == Inf && f[i] > 0) {
dep[v] = dep[u] + 1;
que[tt++] = v;
}
}
}
return (dep[T] != Inf);
}
lf dfs(int u, lf flow) {
if(u == T) {
return flow;
}
lf used = 0;
for(int i = cur[u]; ~i; i = nxt[i]) {
cur[u] = i;
int v = e[i];
if(dep[v] == dep[u] + 1 && f[i] > 0) {
lf low = dfs(v, min(f[i], flow - used));
if(low > 0) {
used += low, f[i] -= low, f[i ^ 1] += low;
if(used == flow) break;
}
else {
dep[v] = Inf;
}
}
}
return used;
}
void Dinic() {
while(bfs() == true) {
flow += dfs(S, Inf);
}
}
bool chk(lf mid) {
flow = 0;
for(int i = 0; i < top; i += 2) {
if(w[i] <= mid) {
flow += w[i] - mid;
f[i] = f[i ^ 1] = 0;
}
else {
f[i] = f[i ^ 1] = w[i] - mid;
}
}
Dinic();
return flow <= 0;
}
int main() {
ios::sync_with_stdio(false);
cin.tie(nullptr), cout.tie(nullptr);
cin >> n >> m >> S >> T;
memset(head, -1, sizeof head);
for(int i = 1; i <= m; ++i) {
int u, v, w;
cin >> u >> v >> w;
add(u, v, w);
}
lf l = 0, r = 1e7, mid, ans;
while(r - l > eps) {
mid = (l + r) / 2;
if(chk(mid) == true) {
r = mid, ans = mid;
}
else {
l = mid;
}
}
cout << fixed << setprecision(2) << ans << '\n';
cout.flush();
return 0;
}
AcWing2280. 最优标号
看到求异或值最大,不难想到拆位求的思路。
把每一位抠出来后,每个点的编号都只能是 $0$ 或 $1$。
那如何把 $0$ 和 $1$ 之间的异或值与割联系起来呢?
考虑到我们如果将割 $[S,T]$ 的 $S$ 集的权值都设为 $0$,$T$ 集的权值都设为 $1$,那么当且仅当只有连接 $0$ 和 $1$ 的边会有贡献,也就是割的割边,所以最小值就是最小割。
注意一些点可能已经被设权值,要提前先加入 $S/T$ 割集中。
#include <bits/stdc++.h>
using namespace std;
typedef long long ll;
const int N = 505, M = 7005, Inf = 0x3f3f3f3f;
int n, m, S, T;
pair<int, int> edge[M];
int a[N];
ll flow;
int head[N], e[M], f[M], nxt[M], top;
int que[N], dep[N], cur[N];
void add(int a, int b, int c) {
e[top] = b, f[top] = c, nxt[top] = head[a], head[a] = top++;
e[top] = a, f[top] = 0, nxt[top] = head[b], head[b] = top++;
}
bool bfs() {
int hh = 0, tt = 1;
memcpy(cur, head, sizeof cur);
memset(dep, 0x3f, sizeof dep);
que[hh] = S, dep[S] = 0;
while(hh != tt) {
int u = que[hh++];
for(int i = head[u]; ~i; i = nxt[i]) {
int v = e[i];
if(dep[v] == Inf && f[i] > 0) {
dep[v] = dep[u] + 1;
que[tt++] = v;
}
}
}
return (dep[T] != Inf);
}
int dfs(int u, int flow) {
if(u == T) {
return flow;
}
int used = 0;
for(int i = cur[u]; ~i; i = nxt[i]) {
cur[u] = i;
int v = e[i];
if(dep[v] == dep[u] + 1 && f[i] > 0) {
int low = dfs(v, min(f[i], flow - used));
if(low > 0) {
used += low, f[i] -= low, f[i ^ 1] += low;
if(used == flow) break;
}
else {
dep[v] = Inf;
}
}
}
return used;
}
void build(int j) {
memset(head, -1, sizeof head); top = 0;
for(int i = 1; i <= m; ++i) {
int u = edge[i].first, v = edge[i].second;
e[top] = v, f[top] = 1, nxt[top] = head[u], head[u] = top++;
e[top] = u, f[top] = 1, nxt[top] = head[v], head[v] = top++;
}
for(int i = 1; i <= n; ++i) {
if(a[i] >= 0) {
if(1 << j & a[i]) {
add(i, T, Inf);
}
else {
add(S, i, Inf);
}
}
}
}
void Dinic(int j) {
build(j);
while(bfs() == true) {
flow += (ll)dfs(S, Inf) << j;
}
}
int main() {
ios::sync_with_stdio(false);
cin.tie(nullptr), cout.tie(nullptr);
cin >> n >> m;
S = 0, T = n + 1;
memset(a, -1, sizeof a);
for(int i = 1; i <= m; ++i) {
cin >> edge[i].first >> edge[i].second;
}
int k;
cin >> k;
while(k--) {
int u, p;
cin >> u >> p;
a[u] = p;
}
for(int j = 0; j < 31; ++j) {
Dinic(j);
}
cout << flow << '\n';
cout.flush();
return 0;
}
最大权闭合图
对于一张图 $G=(V,E)$,每个点有一个点权,我们定义:
一个闭合图指从图中选出一些点构成集合 $S$,使得 $\forall u\in S,(u,v)\in E$,有 $v\in S$,我们可称这样的点集 $S$ 或点集 $S$ 与里面的边集合起来是一个闭合图。
一个闭合图的权是闭合图点集中的点权之和。
最大权闭合图就是所有闭合图中权值最大的那个。
这个问题与最小割有什么联系?我们先说网络建法:对于图中的原先的边,在网络中添加容量为 $Inf$ 的边。对于权值大于 $0$ 的点,再从虚拟源点向这个点连容量为这个点点权大小的边,对于权值小于等于 $0$ 的点,再从这个点向虚拟汇点连容量为这个点点权相反数大小的边。
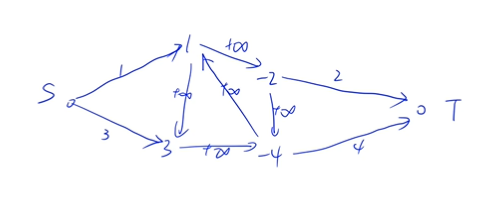
我们定义一个特殊的割叫做简单割,表示所有的割边都跟源点和汇点相连。那么按上述方式建的网络的最小割是不是简单割呢,由最大流最小割定理,最小割等于最大流,而最大流是有限的,则割边不可能包括中间容量为 $Inf$ 的边。
接下来我们要证明闭合图与简单割一一对应。对于一个闭合子图,记它的点集为 $V’$,我们构造割 $[S,T]$,$S={s}+V’,T=V\backslash S+{t}$。而又因为 $V’$ 构成一个闭合图,那么从 $V’$ 中的点怎么走,最终还是只能走到 $V’$ 集合,也就是不可能通过那些容量 $Inf$ 的边从 $S$ 走到 $T$,那么割边不包括容量 $Inf$ 的边,即这是一个简单割。
那么对于一个简单割 $[S,T]$ ,由于不存在容量 $Inf$ 的割边,所以 $S$ 中的点也只能走到 $S$ 中的点,所以是一个闭合图。
那么闭合图的权到底和这个简单割的容量的有什么关系?
设 $S={s}+V_S,T={t}+V_T$,我们看如下四类割边各自造成的贡献:
- $s\rightarrow t$,虚拟源点到虚拟汇点没有直接的边,没有贡献。
- $V_S\rightarrow V_T$,由于是简单割,所以没有贡献。
- $s\rightarrow V_T$,每条割边的容量对应割中的那些正权点的权值,所以这块贡献为正权点权值之和。
- $V_S\rightarrow t$,每条割边的容量对应割中的那些负权点的权值,所以这块贡献为负权点权值之和。
所以最后写成式子就是:$c(S,T)=\sum\limits_{v\in V_T^+}w_v+\sum\limits_{v\in V_S^-}(-w_v)$。
我们去看 $V_S$ 构成的闭合子图的权值:
$w(V_S)=\sum\limits_{v\in V_S^+}w_v-\sum\limits_{v\in V_S^-}(-w_v)$
$=\sum\limits_{v\in V_S^+}w_v+\sum\limits_{v\in V_T^+}w_v-c(S,T)$
$=\sum\limits_{v\in V}w_v-c(S,T)$
则 $V_S$ 的权值是所有点的权值之和减去简单割的容量,那么什么时候有最大值呢,当求得最小割的时候。
至此完成证明。
[NOI2006] 最大获利
本题中如果把建设中转站的费用看作负权点,用户收益看作正权点的话,我们可以转化为最大权闭合图问题。
我们只需向每个用户群和对应的两个中转站连边,当且仅当两个中转站都选了,这个用户群才能选,所以从每个用户群出发得保证走到两个中转站,所以是个闭合子图。
代码:https://www.luogu.com.cn/record/101110660
最大密度子图
对于一个点集 $V$,$E={(u,v)|u\in V, v\in V}$,则这个子图对应密度为 $\dfrac{|E|}{|V|}$,那么如何求对于一个图中的最大密度子图。
看到除法,我们使用 01 分数规划,判定 $\dfrac{|E|}{|V|}\ge g$。
$|E|-g\cdot |V|\ge 0$,我们要最大化 $|E|-g\cdot |V|$,也就是最小化 $g\cdot |V|-|E|$。
$g\cdot |V|-|E|=\sum\limits_{v\in V}g-(\dfrac{\sum\limits_{v\in V}d_v}{2}-\dfrac{c(V,V’)}{2})$,其中 $V’$ 是点的全集和 $V$ 的差集,$d_u$ 是 $u$ 点的度。
我们把系数提到前面得到 $\dfrac{1}{2}(\sum\limits_{v\in V}(g-d_v)+c(V,V’))$,观察到有 $c(V,V’)$ 这样的割的容量的部分,但是我们如何去把前面那项结合起来?
于是有了如下的建图:从源点向每个点连容量为 $U$ 的边,从每个点向汇点连容量为 $U+2g-d_v$ 的边,原图中的边的容量均为 $1$。$U$ 是为了放置边的容量爆负加的偏移量。
我们还是分类算割的容量:
- $s\rightarrow t$,没有,无贡献。
- $s\rightarrow V’$,每条的容量为 $U$。
- $V\rightarrow t$,每条的容量为 $U+2g-d_v$。
- $V\rightarrow V’$,每条的容量均为 $1$。
$c(V,V’)=\sum\limits_{v\in V’}U+\sum\limits_{v\in V}(U+2g-d_v)+\sum\limits_{u\in V}\sum\limits_{v\in V’}c(u,v)$
$=U\cdot n +2g\sum\limits_{v\in V’}1-\sum\limits_{u\in V}\sum\limits_{v\in V}c(u,v)$
$=U\cdot n+2g|V|-2|E|$
这样我们只需最小化 $c(V,V’)$,就能最小化 $g\cdot |V|-|E|$。
最小点权覆盖集
最小点权覆盖集指的是对于一个图 $G$,每个点有权值,找到一个最小的点权和的点集 $V$,使得原图中的每一条边的两个端点都至少 $1$ 个在点集 $V$ 中。
在一般图中,最小点权覆盖集中是 NP-完全问题,但在二分图中,我们可以使用最小割来求解,因此下列所用算法仅适用于二分图。
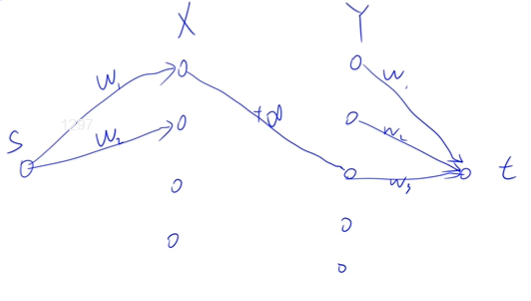
我们对于一个二分图,而如下方式建出网络,由于最小割求的是割边容量的最小值,而最小点权覆盖集对应的是点权值最小,那么我们希望将割边限定在 $S\rightarrow X$ 以及 $Y\rightarrow T$ 的边中,这样我们说一条割边对应了一个需要选择的点,这就解释了我们的建图方式:$S$ 向 $X$ 点集中每个点连容量为每个点权的边,$Y$ 向 $T$ 点集中每个点连容量为每个点权的边,$X$ 向 $Y$ 的边均设定为正无穷,这样割边就不会出现在这里,此时可以证明一个简单割(类似于最大权闭合图的定义,指不包括 $X\rightarrow Y$ 割边的割)对应一个极小的点覆盖集(证明略),而简单割的最小割是所有割的最小割,因此直接在上面的网络找最小割即为答案。
最大点权独立集
最大点权独立集是最小点权覆盖集的对偶问题,当每个点的权值均为 $1$ 时,有最小点权覆盖集 $=$ $n-$ 最大点权独立集。
而当权值不为 $1$ 时,这个结论同样成立,即最小点权覆盖集 $=$ 所有点权和 $-$ 最大点权独立集。
证明从双方向证明:
- 若 $V_1$ 是点覆盖集,那么 $V_2=V-V_1$ 是独立集。
- 若 $V_2$ 是独立集,那么 $V_1=V-V_2$ 是点覆盖集。
用反证法可以轻易的证明出来,因此沿用最小点权覆盖集的方法做即可。
P4474 王者之剑
这题我们先从性质出发:
- 只能在偶数秒捡宝石。我们只需证奇数秒时所在的格子一定没有宝石即可,如果上一秒动了,那么在上一秒时此格子已经被清空,而如果上一秒原地不动,那么此时的宝石应该已经在上一秒被拿走,无论什么情况,奇数秒所在的格子没有宝石,因此只能在偶数秒捡宝石。
- 相邻的格子不可能同时拿到。显然易证。
根据这 $2$ 个性质,不难猜测本题是选择一个独立集。我们将方格图黑白染色,而边都是在黑点和白点之间的,因此图是一个二分图,而不能选相邻的格子就说明我们选择的是一个独立集,本题可以证明一个独立集选择方案能够一一对应一个合法的拿宝石方案,那么这样在最终的网络跑最大点权独立集即可。
代码:https://www.luogu.com.cn/record/101111765
费用流算法
费用流的定义其实非常简单,我们在每条边上添加了一个费用 $w$,表示每单位流量经过这条边所需的花费,那么对于一个网络的某个可行流,我们定义这个可行流的费用为所有边的花费之和。那么我们希望求最小费用最大流/最小流。
$\text{Edmonds Karp}$
在求最大流中,我们使用 bfs() 来找到一条增广路增广,由最大流最小割定理,这个算法是正确的,而对于最小费用最大流,我们只需将 bfs() 换成 spfa(),每次找的是残留网络的最短费用路,然后用这条路增广即可。
注意图中不能出现负环,出现负环请参考P7173 【模板】有负圈的费用流。
时间复杂度
还是 $\mathcal{O}(nm^2)$。总之应该没人卡。
代码
#include <bits/stdc++.h>
using namespace std;
const int N = 5005, M = 100005, Inf = 0x3f3f3f3f;
int n, m, S, T;
int flow, cost;
int head[N], e[M], f[M], w[M], nxt[M], top;
int que[N], dis[N], pre[N], incf[N];
bool inque[N];
void add(int a, int b, int c, int d) {
e[top] = b, f[top] = c, w[top] = d, nxt[top] = head[a], head[a] = top++;
e[top] = a, f[top] = 0, w[top] = -d, nxt[top] = head[b], head[b] = top++;
}
bool spfa() {
int hh = 0, tt = 1;
memset(dis, 0x3f, sizeof dis);
memset(incf, 0, sizeof incf);
que[hh] = S, dis[S] = 0, incf[S] = Inf;
while(hh != tt) {
int u = que[hh++];
if(hh == N) hh = 0;
inque[u] = false;
for(int i = head[u]; ~i; i = nxt[i]) {
int v = e[i];
if(dis[v] > dis[u] + w[i] && f[i] > 0) {
dis[v] = dis[u] + w[i];
pre[v] = i;
incf[v] = min(incf[u], f[i]);
if(inque[v] == false) {
que[tt++] = v;
if(tt == N) tt = 0;
inque[v] = true;
}
}
}
}
return incf[T] > 0;
}
void EdmondsKarp() {
while(spfa() == true) {
int t = incf[T];
flow += t, cost += t * dis[T];
for(int u = T; u != S; u = e[pre[u] ^ 1]) {
f[pre[u]] -= t, f[pre[u] ^ 1] += t;
}
}
}
int main() {
ios::sync_with_stdio(false);
cin.tie(nullptr), cout.tie(nullptr);
cin >> n >> m >> S >> T;
memset(head, -1, sizeof head);
for(int i = 1; i <= m; ++i) {
int a, b, c, d;
cin >> a >> b >> c >> d;
add(a, b, c, d);
}
EdmondsKarp();
cout << flow << ' ' << cost << '\n';
cout.flush();
return 0;
}
$\text{Dinic}$
在 spfa() 后多路增广,复杂度仍为 $\mathcal{O}(nm^2)$,但优化了时间常数。
感觉没啥用就不写了。
费用流相关模型和例题
直接运用
P4015 运输问题
对于每个仓库 $i$,从源点 $S$ 向仓库 $i$ 连容量为 $a_i$,费用为 $0$ 的边;对于每个商店 $j$,从商店 $j$ 向汇点 $T$ 连容量为 $b_j$,费用为 $0$ 的边。
最后,向仓库 $i$ 到商店 $j$ 连容量为 $0$,费用为 $c_{i,j}$ 的边,在此网络上跑最小/最大费用最大流即可。
对于求最大费用最大流,可以将所有边的权值取相反数,求最小费用最大流后将所求费用再求相反数即可。
代码:https://www.luogu.com.cn/record/101131411
P4016 负载平衡问题
首先根据贪心,必定是将高于平均的仓库中货物转到低于平均的仓库。
那么我们从源点 $S$ 向每一个高于平均的仓库连容量为 $a_i-ave$,费用为 $0$ 的边,从每一个低于平均的仓库向汇点连容量为 $ave-a_i$,费用为 $0$ 的边。
最后在相邻两个仓库之间连容量 $Inf$,费用为 $1$ 的边,这样任意一个满流就对应一个合法的搬运方案。
代码:https://www.luogu.com.cn/record/101131507
二分图最优匹配
P4014 分配问题
跟P4015 运输问题差不多,把源点和汇点的边容量都改为 $1$ 就行。
代码:https://www.luogu.com.cn/record/101131608
费用流之最大权不相交路径
P4013 数字梯形问题
针对于路径不相交,我们只需将对应的路径容量设为 $1$,就能保证此边只会被至多一条路径增广。
针对于点不相交,我们想到了在最大流学到的拆点技巧,将其分为入点和出点,在入点和出点连一条容量为 $1$ 的边,这样就能使至多一条路径经过此点。
从不相交改到相交时,注意将相应边的容量放开即可。
代码:https://www.luogu.com.cn/record/101131742
网格图模型
AcWing382. K取方格数
本题中唯一一个难点:“若多条路线重复经过一个格子,只取一次”。也就是说,我们既要保证这个格子能被走多次,还要保证这个格子又一次代价能被计算到。
那么我们可以将格子拆点,从入点向出点连两条边,一条容量为 $Inf$,费用为 $0$,一条容量为 $1$,费用为 $Val_{i,j}$。这样就惊喜的发现解决了我们的要求。
最后我们总结一些建图方式对应的意义:
- 连一条容量为 $Inf$ 的边:某条边可以重复经过。
- 连一条容量为 $1$ 的边:某条边仅能经过 $1$ 次。
- 入点向出点连一条容量为 $1$ 的边:某个点仅能经过 $1$ 次。
- 入点向出点连一条容量为 $Inf$,费用为 $w$ 的边:某个点可经过任意次,且每次经过均有价值 $w$。
- 入点向出点连一条容量为 $1$,费用为 $w$ 的边:某个点只有 $1$ 次价值 $w$ 且仅能经过 $1$ 次。
- 入点向出点连一条容量为 $1$,费用为 $w$ 的边,和一条容量为 $Inf$,费用为 $0$ 的边:某个点可经过任意次,只计算 $1$ 次价值。
#include <bits/stdc++.h>
using namespace std;
const int N = 5005, M = 20005, Inf = 0x3f3f3f3f;
int n, k, S, T;
int cost;
int head[N], e[M], f[M], w[M], nxt[M], top;
int que[N], dis[N], pre[N], incf[N];
bool inque[N];
void add(int a, int b, int c, int d) {
e[top] = b, f[top] = c, w[top] = d, nxt[top] = head[a], head[a] = top++;
e[top] = a, f[top] = 0, w[top] = -d, nxt[top] = head[b], head[b] = top++;
}
bool spfa() {
int hh = 0, tt = 1;
memset(dis, -0x3f, sizeof dis);
memset(incf, 0, sizeof incf);
que[hh] = S, dis[S] = 0, incf[S] = Inf;
while(hh != tt) {
int u = que[hh++];
if(hh == N) hh = 0;
inque[u] = false;
for(int i = head[u]; ~i; i = nxt[i]) {
int v = e[i];
if(dis[v] < dis[u] + w[i] && f[i] > 0) {
dis[v] = dis[u] + w[i];
pre[v] = i;
incf[v] = min(incf[u], f[i]);
if(inque[v] == false) {
que[tt++] = v;
if(tt == N) tt = 0;
inque[v] = true;
}
}
}
}
return incf[T] > 0;
}
void EdmondsKarp() {
while(spfa() == true) {
int t = incf[T];
cost += t * dis[T];
for(int u = T; u != S; u = e[pre[u] ^ 1]) {
f[pre[u]] -= t, f[pre[u] ^ 1] += t;
}
}
}
inline int get(int x, int y) {
return (x - 1) * n + y;
}
int main() {
ios::sync_with_stdio(false);
cin.tie(nullptr), cout.tie(nullptr);
cin >> n >> k;
memset(head, -1, sizeof head);
S = 0, T = 1;
add(S, get(1, 1) * 2, k, 0);
for(int i = 1; i <= n; ++i) {
for(int j = 1; j <= n; ++j) {
int c;
cin >> c;
add(get(i, j) * 2, get(i, j) * 2 + 1, 1, c);
add(get(i, j) * 2, get(i, j) * 2 + 1, Inf, 0);
if(i + 1 <= n) add(get(i, j) * 2 + 1, get(i + 1, j) * 2, Inf, 0);
if(j + 1 <= n) add(get(i, j) * 2 + 1, get(i, j + 1) * 2, Inf, 0);
}
}
add(get(n, n) * 2 + 1, T, k, 0);
EdmondsKarp();
cout << cost << '\n';
cout.flush();
return 0;
}
AcWing2195. 深海机器人问题
我们考虑对于每个初始有机器人的格子作为出发点连源点 $S$,而目的地作为结束点连汇点 $T$。而题目要求“到达目的地的机器人尽可能多的情况下,最高收益是多少”,那么我们自然将其对应为最大费用最大流,我们把网格上相邻的边对应到网络中边的费用即可。
#include <bits/stdc++.h>
using namespace std;
const int N = 270, M = 2000, Inf = 0x3f3f3f3f;
int a, b, n, m, S, T;
int cost;
int head[N], e[M], f[M], w[M], nxt[M], top;
int que[N], dis[N], pre[N], incf[N];
bool inque[N];
void add(int a, int b, int c, int d) {
e[top] = b, f[top] = c, w[top] = d, nxt[top] = head[a], head[a] = top++;
e[top] = a, f[top] = 0, w[top] = -d, nxt[top] = head[b], head[b] = top++;
}
bool spfa() {
int hh = 0, tt = 1;
memset(dis, -0x3f, sizeof dis);
memset(incf, 0, sizeof incf);
que[hh] = S, dis[S] = 0, incf[S] = Inf;
while(hh != tt) {
int u = que[hh++];
if(hh == N) hh = 0;
inque[u] = false;
for(int i = head[u]; ~i; i = nxt[i]) {
int v = e[i];
if(dis[v] < dis[u] + w[i] && f[i] > 0) {
dis[v] = dis[u] + w[i];
pre[v] = i;
incf[v] = min(incf[u], f[i]);
if(inque[v] == false) {
que[tt++] = v;
if(tt == N) tt = 0;
inque[v] = true;
}
}
}
}
return incf[T] > 0;
}
void EdmondsKarp() {
while(spfa() == true) {
int t = incf[T];
cost += t * dis[T];
for(int u = T; u != S; u = e[pre[u] ^ 1]) {
f[pre[u]] -= t, f[pre[u] ^ 1] += t;
}
}
}
inline int get(int x, int y) {
return x * (m + 1) + y;
}
int main() {
ios::sync_with_stdio(false);
cin.tie(nullptr), cout.tie(nullptr);
cin >> a >> b >> n >> m;
memset(head, -1, sizeof head);
S = (n + 1) * (m + 1) + 1, T = (n + 1) * (m + 1) + 2;
for(int i = 0; i < n + 1; ++i) {
for(int j = 0; j < m; ++j) {
int c;
cin >> c;
add(get(i, j), get(i, j + 1), 1, c);
add(get(i, j), get(i, j + 1), Inf, 0);
}
}
for(int j = 0; j < m + 1; ++j) {
for(int i = 0; i < n; ++i) {
int c;
cin >> c;
add(get(i, j), get(i + 1, j), 1, c);
add(get(i, j), get(i + 1, j), Inf, 0);
}
}
for(int i = 1; i <= a; ++i) {
int k, x, y;
cin >> k >> x >> y;
add(S, get(x, y), k, 0);
}
for(int i = 1; i <= b; ++i) {
int r, x, y;
cin >> r >> x >> y;
add(get(x, y), T, r, 0);
}
EdmondsKarp();
cout << cost << '\n';
cout.flush();
return 0;
}
拆点
P1251 餐巾计划问题
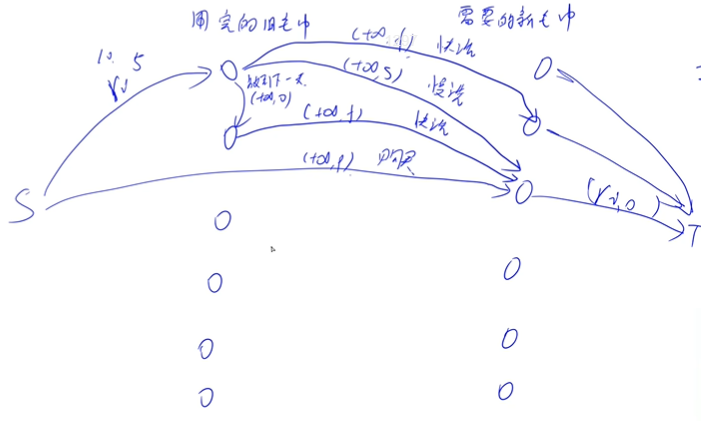
本题中要注意我们将每一天的餐巾拆分为“用完的旧餐巾”和“需要的新餐巾”,然后我们对于“需要的新餐巾”向汇点连容量 $r_i$,费用为 $0$ 的边,因此我们限制了“需要的新餐巾”数量,从而使任意一个满流对应了一个餐巾 的方案,跑最小费用最大流即可。
而其余的不同情况的连边,参考下图。
代码:https://www.luogu.com.cn/record/101132505
无源汇有上下界最小费用可行流问题
P3980 [NOI2008] 志愿者招募
我们先按如下方式建出网络:
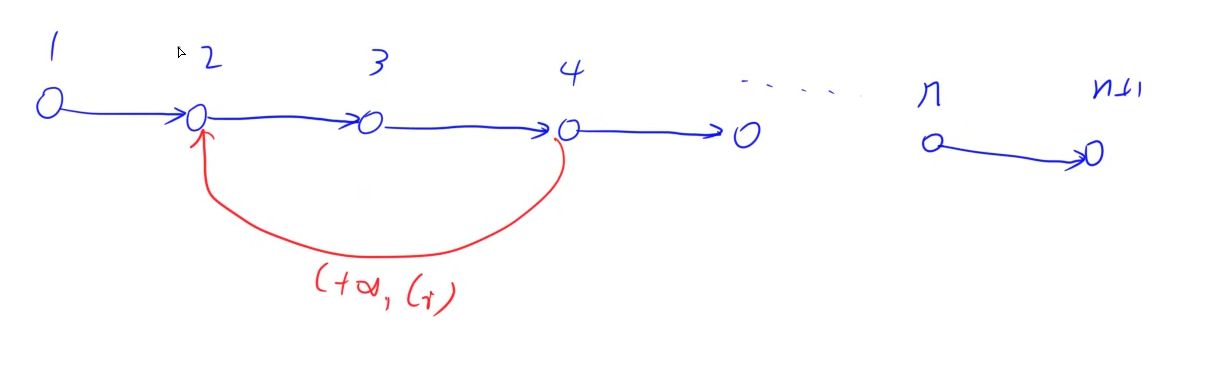
其中第 $i$ 号点和 $(i+1)$ 号点的边就表示第 $i$ 天志愿者变化的人数。(可以为负值)
红色的边是指每类志愿者的工作区间 $[s_i,t_i]$ 会在边上凭空产生 $1$ 的流量,为了满足流量守恒,我们建反边形成回路就能平衡流量。
那么我们说每条边的容量均有下界值,因为如果小于下界,那么下一天的志愿者人数就不能满足要求。这是一个无源汇有上下界最小费用可行流问题,如何求解?
参考无源汇有上下界可行流的做法,我们对于每个点,统计进入这个点的容量 $c_入$ 和流出这个点的容量 $c_出$,若 $c_入>c_出$,从 $S$ 到这个点连容量 $c_入-c_出$ 的边,反之从这个点向 $T$ 连容量 $c_出-c_入$ 的边即满足流量守恒。当然本题实际上我们是把每条边看作一个新网络上的点,而 $c_入$ 就是这个边左边的端点对应的人数,$c_出$ 就是这个边右边的端点对应的人数。
对按这种方式建成的新网络求最小费用最大流就是原问题的答案。