$\text{KMP}$
概念
子串
在 CF 的题目中比较常见,我们可以直接引用:
A string $a$ is a substring of a string $b$ if $a$ can be obtained from $b$ by deletion of several (possibly, zero or all) characters from the beginning and several (possibly, zero or all) characters from the end.
简单的说,就是字符串中的连续一段字符,对于一个字符串 $s$,记其中的 $l\sim r$ 段为 $s(l,r)$。
前缀
对于一个字符串 $s$,记前 $k$ 个字符构成的子串为 $pre(s,k)$。
后缀
对于一个字符串 $s$,记后 $k$ 个字符构成的子串为 $suf(s,k)$。
最长公共前缀
对于字符串 $s,t$,记 $s,t$ 的最长的完全相同的前缀长度为 $lcp(s,t)$。
接下来是关于 $\text{KMP}$ 涉及到的概念。
周期
- $0<p<|s|$
- $\forall i\in [1,|s|-p],s_i=s_{i+p}$
- 满足以上条件,称 $p$ 为 $s$ 的周期。

$\text{Border}$
- $0<r<|s|$
- $pre(s,r)=suf(s,r)$
- 满足以上条件,称 $pre(s,r)$ 是 $s$ 的 $\text{Border}$,所以 $\text{Border}$ 指的仍是一个字符串。

【重要结论】 $pre(s,k)$ 是 $s$ 的 $\text{Border}$ $\Leftrightarrow$ $|s|-k$ 是 $s$ 的周期
举个例子,我们假设下图的蓝色部分是一个 $\text{Border}$:
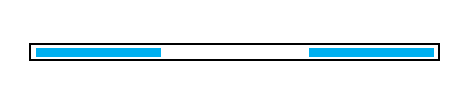
那么红色就一定是一个满足要求的周期,反过来也同样成立。
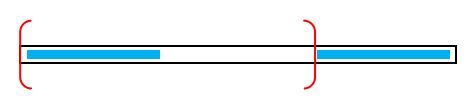
*$\text{Border}$ 的传递性
这个也是十分重要的结论。串 $s$ 是 $t$ 的 $\text{Border}$,串 $t$ 是 $r$ 的 $\text{Border}$,那么 $s$ 是 $r$ 的 $\text{Border}$。

一个更强的传递性:若串 $s$ 是 $r$ 的 $\text{Border}$,串 $t$ 是 $r$ 的 $\text{Border}$,且 $|t|>|s|$ ,那么有 $s$ 是 $t$ 的 $\text{Border}$。
有了这个性质,我们就能得到,如果向 $s$ 和它的最长 $\text{Border}$ 连边,那么对于 $s$ 的所有 $\text{Border}$,其一定构成了一条由 $s$ 到以空串结尾的一条链,且长度严格递减。这是 $\text{KMP}$ 正确性的前提。
算法流程
$\text{KMP}$ 主要是为了求出 $nxt$ 数组,其中 $nxt_i$ 表示 $pre(s,i)$ 的最长 $\text{Border}$ 的长度,
我们在循环 $i=1\rightarrow n$ 时,同时记录一个临时变量 $j$,代表 $i-1$ 时能匹配 $\text{Border}$ 的最长长度 $j$,那么我们有 $s(i - j, i - 1)=pre(s,j)$。
那么我们如何求出当前的 $j$ 呢?考虑如果我们想增大 $j$,则我们需要使下一个位置的字符继续保持匹配,即 $s_i=s_{j+1}$。
当我们不能匹配时,我们通过不断的跳 $nxt$ 使得出现 $s_i=s_{j+1}$,那么代码即为:
nxt[1] = 0;
for(int i = 2, j = 0;i <= n;i++) {
while(j > 0 && str[j + 1] != str[i]) {
j = nxt[j];
}
if(str[j + 1] == str[i]) {
j++;
}
nxt[i] = j;
}
我们需要说明两个问题来证明正确性:
为什么这样求出的 $nxt_i$ 是最长的?
首先我们有,如果 $pre(s,j)$ 是 $pre(s,i)$ 的 $\text{Border}$,那么就一定有等价于 $pre(s,j-1)$ 是 $pre(s,i-1)$ 的 $\text{Border}$。
设
while()停止时的 $j$ 为 $j_0$,那么 $j_0$ 一定是满足 $s_{j_0+1}=s_i$ 的 $pre(s,i-1)$ 的最长 $\text{Border}$,而这个满足的最长 $pre(s,i-1)$ 的 $\text{Border}$ 就可以转化为 $pre(s,i)$ 的最长 $\text{Border}$。为什么下面的
if只需要判断一次(即不用也改成while())?这个根据上面其实比较好推出。找到最大的 $j_0$ 后,最多只会往后匹配一个字符。如果能匹配超过一个字符,则我们的 $j_0$ 一定还会增大,因为此时这个更长的也会成为 $pre(s,i-1)$ 的更长的 $\text{Border}$ 且满足 $s_i=s_{j_0+1}$。
那么解决了这两个问题,我们就可以分析一下时间复杂度。在 while() 中,$j$ 每次严格减小 $1$ 且减到 $0$ 后不再减小;在 if 中,$j$ 每次最多增加 $1$。所以 $j$ 的变化次数是 $\mathcal{O}(n)$,最终的时间复杂度是 $\mathcal{O}(n)$ 的。
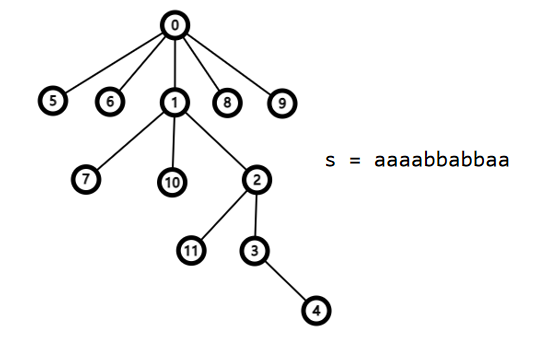
失配树
将 $nxt_i$ 视为 $i$ 的父节点,那么一个 $nxt$ 数组就对应了一个节点编号为 $0\sim n$ 的数。
- 点 $i$ 的所有祖先都是前缀 $pre(s,i)$ 的 $\text{Border}$
- 没有祖先关系的两个点 $i,j$ 没有 $\text{Border}$ 关系
- $u$ 和 $v$ 在失配树的最近公共祖先就是 $pre(s,u)$ 和 $pre(s,v)$ 最长公共 $\text{Border}$。
$\text{AC-automaton}$
AC 自动机,本质上是字典树和 $fail$ 指针构成。
简单说一下 AC 自动机的构建方法:
- 对模式串建出 trie 树
- 用 bfs 建出 $fail$ 指针
void buildFail() {
queue<int> que;
for(int ch = 0;ch < 26;ch++) {
if(trie[rt][ch] != 0) {
que.push(trie[rt][ch]);
}
else {
trie[rt][ch] = rt;
}
fail[trie[rt][ch]] = rt;
}
while(!que.empty()) {
int u = que.front(); que.pop();
for(int ch = 0;ch < 26;ch++) {
if(trie[u][ch] != 0) {
fail[trie[u][ch]] = trie[fail[u]][ch];
que.push(trie[u][ch]);
}
else {
trie[u][ch] = trie[fail[u]][ch]; // 注意这里执行的是类似路径压缩的操作
}
}
}
}
$fail$ 的性质
当我们走到了 trie 树上的点 $p$ 时,那么匹配模式串的数量就是 fail 树上 $p$ 到 $rt$ 的点的个数。
可以用来维护一类 $fail$ 树上的子树修改等问题。
习题
P5829【模板】失配树
建出失配树,对于一组询问 $(u,v)$,我们找其最近公共祖先即可,注意 $\text{Border}$ 长度严格小于这个串,所以是祖先关系的话需要再向上跳一个点。
时间复杂度 $\mathcal{O}(n+m\log n)$。
代码
#include <bits/stdc++.h>
using namespace std;
int n, q;
char str[1000005];
int nxt[1000005];
int dep[1000005], lg[1000005], anc[1000005][21];
int getlca(int u, int v) {
if(dep[u] < dep[v]) {
swap(u, v);
}
while(dep[u] > dep[v]) {
int j = lg[dep[u] - dep[v]];
u = anc[u][j];
}
if(u == v) {
return u;
}
for(int j = lg[dep[u]];j >= 0;j--) {
if(anc[u][j] != anc[v][j]) {
u = anc[u][j], v = anc[v][j];
}
}
return anc[u][0];
}
int main() {
ios::sync_with_stdio(false);
cin.tie(nullptr), cout.tie(nullptr);
cin >> (str + 1);
n = strlen(str + 1);
lg[0] = -1;
for(int i = 1;i <= n + 1;i++) {
lg[i] = lg[i / 2] + 1;
}
nxt[1] = 0;
for(int i = 2, j = 0;i <= n;i++) {
while(j > 0 && str[j + 1] != str[i]) {
j = nxt[j];
}
if(str[j + 1] == str[i]) {
j++;
}
nxt[i] = j;
}
for(int i = 1;i <= n;i++) {
dep[i] = dep[nxt[i]] + 1;
}
for(int i = 0;i <= n;i++) {
anc[i][0] = nxt[i];
}
for(int j = 1;(1 << j) <= n;j++) {
for(int i = 0;i <= n;i++) {
anc[i][j] = anc[anc[i][j - 1]][j - 1];
}
}
cin >> q;
while(q--) {
int u, v, lca;
cin >> u >> v;
lca = getlca(u, v);
if(lca == u || lca == v) {
lca = nxt[lca];
}
cout << lca << '\n';
}
cout.flush();
return 0;
}
P3426 [POI2005] SZA-Template
首先需要考虑到什么样的印章是合法的,首先我们的印章必定是一个前缀,这就引导我们考虑与 $nxt$ 的关系,假设印章为 $pre(s,j)$,那么对于所有能盖章的结尾位置 $i$,那么 $pre(s,j)$ 一定是 $pre(s,i)$ 的 $\text{Border}$,即 $pre(s,j)=s(i-j+1,i)$。那么对于每一个合法的印章,则我们需要使所有能盖章的位置之间的任意两两距离都不超过 $j$ 才行。当然 $pre(s,j)$ 还必须是 $s$ 的 $\text{Border}$。
那么转化到失配树上,答案所对应的节点 $u$ 有如下性质:
- 在 $0\rightarrow n$ 的链上
- $u$ 的子树内所有点在值域上相邻之差不超过 $u$
考虑这是单调的,那么我们可以从 $0$ 往下走,把其它子树的节点在值域数据结构中删掉,维护最大值,判断是否超过 $u$,而因为只需支持删除且答案单调不降,使用链表维护。
时间复杂度 $\mathcal{O}(n)$。
代码
#include <bits/stdc++.h>
using namespace std;
int n;
char str[500005];
vector<int> adj[500005];
int father[500005]; // nxt
int res = 1;
int pre[500005], nxt[500005];
int lisT[500005], t; // 0 -> n
void del(int q) {
if(nxt[q] != 1e9 && pre[q] != 1e9) res = max(res, nxt[q] - pre[q]);
if(pre[q] != 1e9) nxt[pre[q]] = nxt[q];
if(nxt[q] != 1e9) pre[nxt[q]] = pre[q];
}
void dfs(int u, int p) {
del(u);
for(int v: adj[u]) {
if(v == p) {
continue;
}
dfs(v, p);
}
}
int main() {
ios::sync_with_stdio(false);
cin.tie(nullptr), cout.tie(nullptr);
cin >> (str + 1);
n = strlen(str + 1);
father[1] = 0; adj[0].push_back(1);
for(int i = 2, j = 0;i <= n;i++) {
while(j > 0 && str[j + 1] != str[i]) {
j = father[j];
}
if(str[j + 1] == str[i]) {
j++;
}
father[i] = j; adj[j].push_back(i);
}
for(int i = 0;i <= n;i++) {
pre[i] = (i == 0) ? 1e9 : i - 1;
nxt[i] = (i == n) ? 1e9 : i + 1;
}
for(int u = n;u != 0;u = father[u]) {
lisT[++t] = u;
}
reverse(lisT + 1, lisT + t + 1);
for(int i = 1;i <= t;i++) {
int u = lisT[i];
dfs(father[u], u);
if(res <= u) {
cout << u << '\n';
return 0;
}
}
cout.flush();
return 0;
}
P2375 [NOI2014] 动物园
转化的失配树上,则每个节点 $i$ 所对应的答案,是 $0\rightarrow i$ 的一段前缀,在树上倍增寻找最大的符合要求就能解决,时间复杂度 $\mathcal{O}(n\log n)$,有没有更优的做法。
考虑 $\text{KMP}$ 的具体意义,求 $pre(s,i)$ 的最长 $\text{Border}$。那么我们修改一下,改为求 $pre(s,i)$ 的最长且不超过 $\lfloor\dfrac{i}{2}\rfloor$ 的 $\text{Border}$,是否仍然可以递推。
答案是可以的,根据原 $\text{KMP}$ 算法的分析,我们很容易证明新的 $j’$ 会是下一个串的新 $\text{Border}$,而长度自然也是可以满足的,$\lfloor\dfrac{i}{2}\rfloor+1\geq \lfloor\dfrac{i+1}{2}\rfloor$,那么往后至多 $1$ 个即能找到最长的符合的 $\text{Border}$,记录一下 $dep_i$ 表示 $0\rightarrow i$ 上点的数量就行。
时间复杂度 $\mathcal{O}(n)$。
代码
nxt[1] = 0, dep[1] = 1;
for(int i = 2, j = 0;i <= n;i++) {
while(j > 0 && str[j + 1] != str[i]) {
j = nxt[j];
}
if(str[j + 1] == str[i]) {
j++;
}
nxt[i] = j, dep[i] = dep[j + 1];
}
for(int i = 2, j = 0;i <= n;i++) {
while(j > 0 && str[j + 1] != str[i]) {
j = nxt[j];
}
if(str[j + 1] == str[i]) {
j++;
}
while(j * 2 > i) {
j = nxt[j];
}
ans = (ans * (dep[j] + 1)) % Mod;
}
P3435 [POI2006] OKR-Periods of Words
由于一个 $\text{Border}$ 对应一个周期,根据题意,我们可以得知 $pre(s,i)$ 周期的长度区间为 $[\lceil\dfrac{i}{2}\rceil,i)$,那么 $\text{Border}$ 所对应的长度区间为 $(0,i-\lceil\dfrac{i}{2}\rceil]$,即失配树上根的一段路径。
可以 $\mathcal{O}(n\log n)/\mathcal{O}(n)$ 解决。
代码
#include <bits/stdc++.h>
using namespace std;
typedef long long ll;
int n;
char str[1000005];
int nxt[1000005];
ll ans;
int main() {
ios::sync_with_stdio(false);
cin.tie(nullptr), cout.tie(nullptr);
cin >> n >> (str + 1);
nxt[1] = 0;
for(int i = 2, j = 0;i <= n;i++) {
while(j > 0 && str[j + 1] != str[i]) {
j = nxt[j];
}
if(str[j + 1] == str[i]) {
j++;
}
nxt[i] = j;
}
for(int i = 2;i <= n;i++) {
int j = i;
while(nxt[j] > 0) {
j = nxt[j];
}
if(nxt[i] > 0){
nxt[i] = j;
}
ans += (i - j);
}
cout << ans << '\n';
cout.flush();
return 0;
}
P3193 [HNOI2008] GT考试
考虑什么样的串 $X$ 不能完全匹配一个串 $A$,也就是用 $X$ 串跑 $\text{KMP}$ 时,不存在任意一个 $i$,使得 $X(i-m+1,i)=A$。
那么我们可以通过记录状态的方式,表示当前与 $X$ 串的匹配长度,这样我们可以使用 $\text{KMP}$ 更新下一位的匹配位置。
记录 $f_{j,c}$ 的值为 $j_0$,表示当前 $A$ 串的 $j$ 位与 $X$ 串的前 $j$ 位完全匹配时,在 $A$ 串后面加一个字符 $c$ 后新的匹配长度为 $j_0$。
那么 $dp_{i,j}$ 表示 $A$ 的前 $i$ 位中,最后的 $j$ 个字符与 $X$ 串的前 $j$ 为完全匹配时的方案数。那么枚举一个转移字符 $c$,有转移方程:$dp_{i,j}\stackrel{c}\rightarrow dp_{i+1,f_{j,c}}$。
由于我们最终不能有满足完全匹配的 $A$ 串,那么在转移的时候,任何转移到 $dp_{i,m}$ 的转移都不能在答案的计算之内,所以我们可只在 $j\in [0,m)$ 转移,最终答案为 $\sum\limits_{0\leq j<m}dp_{n,j}$。
观察到转移与 $i$ 无关,可用矩阵快速幂加速。
最终复杂度 $\mathcal{O}(26m^2+m^3\log n)$。
代码
#include <bits/stdc++.h>
using namespace std;
int n, m, p;
char str[25];
int nxt[25];
int ans;
struct Mat {
int num[20][20];
Mat() {
memset(num, 0, sizeof(num));
}
Mat operator * (const Mat &A) const {
Mat res;
for(int i = 0;i < m;i++) {
for(int j = 0;j < m;j++) {
for(int k = 0;k < m;k++) {
res.num[i][j] += num[i][k] * A.num[k][j];
}
res.num[i][j] %= p;
}
}
return res;
}
};
Mat Matpow(Mat A, int b) {
Mat base = A, res;
for(int i = 0;i < m;i++) {
res.num[i][i] = 1;
}
while(b) {
if(b & 1) res = res * base;
b >>= 1;
base = base * base;
}
return res;
}
int F[20], G[20];
int main() {
ios::sync_with_stdio(false);
cin.tie(nullptr), cout.tie(nullptr);
cin >> n >> m >> p;
cin >> (str + 1);
nxt[1] = 0;
for(int i = 2, j = 0;i <= m;i++) {
while(j > 0 && str[j + 1] != str[i]) {
j = nxt[j];
}
if(str[j + 1] == str[i]) {
j++;
}
nxt[i] = j;
}
Mat A, B;
for(int i = 0;i < m;i++) {
for(char c = '0';c <= '9';c++) {
int j = i;
while(j > 0 && str[j + 1] != c) {
j = nxt[j];
}
if(str[j + 1] == c) {
j++;
}
A.num[j][i]++;
}
}
B = Matpow(A, n);
F[0] = 1;
for(int i = 1;i < m;i++) {
F[i] = 0;
}
for(int i = 0;i < m;i++) {
for(int k = 0;k < m;k++) {
G[i] += F[k] * B.num[i][k];
}
ans += G[i] % p;
}
cout << ans % p << '\n';
cout.flush();
return 0;
}
U194290 【HDOI2021提高组T2】
本题你正着看这个串十分难办,因为串都是动的且无法跟一段前缀扯上关系。
但当你注意到四元组 $(l,r,x,y)$ 的条件之一是 $s(n-len+1,n)=s(l,r)=s(x,y)$。
看到 $s(n-len+1,n)$,说明一个四元组需要对应与字符串后缀相同,能不能转化成 $\text{Border}$ 呢?
可以。将串翻转后,我们将四元组 $(l,r,x,y)$ 等价于 $s’(1,len)=s‘(l,r)=s’(x,y)$,$r<y$,权值为 $|w_r-w_y|$。
那么当 $pre(s’,r)$ 和 $pre(s’,y)$ 都有 $pre(s’,len)$ 这个 $\text{Border}$ 时就是一个合法的四元组 $(l,r,x,y)$ 的充要条件(不考虑 $r<y$ 的情况下),对应到失配树上就是一个节点 $u$ 的子树内任意两个节点都构成四元组,如果加上 $r<y$ 就是任意两个点构成的有序点对构成一个四元组。
对于每个节点的 $u$ 的子树内都要查询,使用线段树合并维护信息即可。
线段树支持插入、合并、查询值域相邻两点最小值、查询值域上有序点对的差的和。(因为 $|w_r-w_y|=|w_y-w_r|$,所以统计有序的差的和恰好就是任意两个有序点差的绝对值的总和)
时间复杂度 $\mathcal{O}(n\log n)$,空间复杂度 $\mathcal{O}(n\log n)$,空间常数很大。
代码
#include <bits/stdc++.h>
using namespace std;
typedef long long ll;
const int Mod = 20050801;
int n;
int w[500005];
char str[500005];
int nxt[500005];
vector<int> adj[500005];
ll mi = 1e10, res;
int rt[500005], node;
struct SegMent {
int l, r, cnt, ml, mr, mi, sum, res;
}tree[15500005];
inline int ls(int p) {return tree[p].l;}
inline int rs(int p) {return tree[p].r;}
void pushup(int p) {
tree[p].ml = (tree[ls(p)].ml == 0) ? tree[rs(p)].ml : tree[ls(p)].ml;
tree[p].mr = (tree[rs(p)].mr == 0) ? tree[ls(p)].mr : tree[rs(p)].mr;
tree[p].mi = 2e9;
if(tree[ls(p)].cnt >= 2) {
tree[p].mi = min(tree[p].mi, tree[ls(p)].mi);
}
if(tree[rs(p)].cnt >= 2) {
tree[p].mi = min(tree[p].mi, tree[rs(p)].mi);
}
if(tree[ls(p)].mr != 0 && tree[rs(p)].ml != 0) {
tree[p].mi = min(tree[p].mi, tree[rs(p)].ml - tree[ls(p)].mr);
}
tree[p].cnt = tree[ls(p)].cnt + tree[rs(p)].cnt;
tree[p].sum = (tree[ls(p)].sum + tree[rs(p)].sum) % Mod;
tree[p].res = tree[ls(p)].res + tree[rs(p)].res + 1ll * tree[ls(p)].cnt * tree[rs(p)].sum % Mod - 1ll * tree[rs(p)].cnt * tree[ls(p)].sum % Mod;
tree[p].res = (tree[p].res % Mod + Mod) % Mod;
}
int upd(int p, int l, int r, int x) {
if(p == 0) {
p = ++node;
}
if(l == r) {
tree[p].cnt++;
tree[p].sum = (tree[p].sum + l) % Mod;
tree[p].ml = tree[p].mr = l;
if(tree[p].cnt <= 1) tree[p].mi = 2e9;
else tree[p].mi = 0;
}
else {
int mid = (l + r) >> 1;
if(x <= mid) {
tree[p].l = upd(ls(p), l, mid, x);
}
else {
tree[p].r = upd(rs(p), mid + 1, r, x);
}
pushup(p);
}
return p;
}
int merge(int p1, int p2, int l, int r) {
if(p1 == 0 || p2 == 0) {
return p1 + p2;
}
if(l == r) {
tree[p1].cnt += tree[p2].cnt;
tree[p1].sum = (tree[p1].sum + tree[p2].sum) % Mod;
tree[p1].ml = tree[p1].mr = l;
if(tree[p1].cnt <= 1) tree[p1].mi = 2e9;
else tree[p1].mi = 0;
}
else {
int mid = (l + r) >> 1;
tree[p1].l = merge(ls(p1), ls(p2), l, mid);
tree[p1].r = merge(rs(p1), rs(p2), mid + 1, r);
pushup(p1);
}
return p1;
}
void dfs(int u) {
for(int v: adj[u]) {
dfs(v);
rt[u] = merge(rt[u], rt[v], 1, 1e9);
}
if(u != 0) {
rt[u] = upd(rt[u], 1, 1e9, w[u]);
mi = min(mi, (ll)tree[rt[u]].mi);
res += tree[rt[u]].res;
}
}
int main() {
ios::sync_with_stdio(false);
cin.tie(nullptr), cout.tie(nullptr);
cin >> n >> (str + 1);
for(int i = 1;i <= n;i++) {
cin >> w[i];
}
reverse(str + 1, str + n + 1);
reverse(w + 1, w + n + 1);
nxt[1] = 0; adj[0].push_back(1);
for(int i = 2, j = 0;i <= n;i++) {
while(j > 0 && str[j + 1] != str[i]) {
j = nxt[j];
}
if(str[j + 1] == str[i]) {
j++;
}
nxt[i] = j; adj[j].push_back(i);
}
dfs(0);
if(mi >= 1e9) mi = -1;
cout << mi << ' ' << res % Mod << '\n';
cout.flush();
return 0;
}
P5357 【模板】AC 自动机(二次加强版)
建出 AC 自动机后,拿文本串在 AC 自动机上跑一遍,然后在 $fail$ 树上做子树求和,最后对于每个模式串,输出结尾节点上的权值即可。
时间复杂度 $\mathcal{O}(|S|+|T|)$。
代码
#include <bits/stdc++.h>
using namespace std;
int n;
char str[200005], t[2000005];
int trie[200005][26], ed[5200005], rt = 1, tot = 1;
vector<int> adj[5200005];
int fail[5200005];
int bucket[5200005];
int ans[200005];
void ins(int s) {
int p = rt;
for(int i = 1, m = strlen(str + 1);i <= m;i++) {
int ch = str[i] - 'a';
if(trie[p][ch] == 0) {
trie[p][ch] = ++tot;
}
p = trie[p][ch];
}
ed[s] = p;
}
void buildFail() {
queue<int> que;
for(int ch = 0;ch < 26;ch++) {
if(trie[rt][ch] != 0) {
que.push(trie[rt][ch]);
}
else {
trie[rt][ch] = rt;
}
fail[trie[rt][ch]] = rt;
}
while(!que.empty()) {
int u = que.front(); que.pop();
for(int ch = 0;ch < 26;ch++) {
if(trie[u][ch] != 0) {
fail[trie[u][ch]] = trie[fail[u]][ch];
que.push(trie[u][ch]);
}
else {
trie[u][ch] = trie[fail[u]][ch];
}
}
}
}
void dfs(int u) {
ans[u] = bucket[u];
for(int v: adj[u]) {
dfs(v);
ans[u] += ans[v];
}
}
int main() {
ios::sync_with_stdio(false);
cin.tie(nullptr), cout.tie(nullptr);
cin >> n;
for(int i = 1;i <= n;i++) {
cin >> (str + 1);
ins(i);
}
buildFail();
cin >> (t + 1);
int p = rt;
for(int i = 1, m = strlen(t + 1);i <= m;i++) {
int ch = t[i] - 'a';
p = trie[p][ch]; bucket[p]++;
}
for(int i = 2;i <= tot;i++) {
adj[fail[i]].push_back(i);
}
dfs(rt);
for(int s = 1;s <= n;s++) {
cout << ans[ed[s]] << '\n';
}
cout.flush();
return 0;
}
P2444 [POI2000] 病毒
将所有病毒代码段在 trie 上的结尾节点的子树禁掉,那么存在无限代码段的充要条件就是在 AC自动机上通过未被禁掉的节点走出一个环。
判环使用 $vis$ 标颜色即可。
时间复杂度 $\mathcal{O}(|S|)$。
代码
#include <bits/stdc++.h>
using namespace std;
int n;
char str[30005];
int trie[30005][2], rt = 1, tot = 1;
int fail[60005], vis[60005];
bool visu[60005];
void ins() {
int p = rt;
for(int i = 1, m = strlen(str + 1);i <= m;i++) {
int ch = str[i] - '0';
if(trie[p][ch] == 0) {
trie[p][ch] = ++tot;
}
p = trie[p][ch];
}
vis[p] = true;
}
void buildFail() {
queue<int> que;
for(int ch = 0;ch < 2;ch++) {
if(trie[rt][ch] != 0) {
que.push(trie[rt][ch]);
}
else {
trie[rt][ch] = rt;
}
fail[trie[rt][ch]] = rt;
}
while(!que.empty()) {
int u = que.front(); que.pop();
for(int ch = 0;ch < 2;ch++) {
if(trie[u][ch] != 0) {
fail[trie[u][ch]] = trie[fail[u]][ch]; vis[trie[u][ch]] |= vis[fail[trie[u][ch]]];
que.push(trie[u][ch]);
}
else {
trie[u][ch] = trie[fail[u]][ch];
}
}
}
}
bool dfs(int u) {
if(visu[u] == true) {
return true;
}
visu[u] = true;
for(int ch = 0;ch < 2;ch++) {
if(trie[u][ch] != 0 && vis[trie[u][ch]] == false && dfs(trie[u][ch]) == true) {
return true;
}
}
visu[u] = false;
return false;
}
int main() {
ios::sync_with_stdio(false);
cin.tie(nullptr), cout.tie(nullptr);
cin >> n;
for(int i = 1;i <= n;i++) {
cin >> (str + 1);
ins();
}
buildFail();
cout << (dfs(rt) == true ? "TAK" : "NIE") << '\n';
cout.flush();
return 0;
}
P2414 [NOI2011] 阿狸的打字机
$70$ 分做法:
所有串的长度加起来 $\leq 10^5$,故可以每一个串暴力在 AC 自动机上跑,更新其它串的答案,注意每次还需将上次跑的串清空。
时间复杂度 $\mathcal{O}(|S|+q\log |S|)$。
$100$ 分做法:
我们观察到打字机打出的字符长度同样 $\leq 10^5$,由于 P 操作不会影响下一个串在 trie 上的位置,所以 trie 中的节点数量 $\leq 10^5$,那么有没有办法不一个一个扫串统计答案?
观察到相邻的两个串的变化只有新加一个字符和 B 操作,B 操作可理解为回到 trie 的父节点,那么我们可以对于输入实时维护当前串的答案,加入字符是单点加,B 操作是单点减,最后有关这个串的询问就是 $fail$ 树上子树查询,用树状数组维护即可。
时间复杂度 $\mathcal{O(n+q\log n)}$。
代码
#include <bits/stdc++.h>
using namespace std;
char str[100005];
int n, pos[2600005];
int q;
int trie[100005][26], ed[100005], father[2600005], rt = 1, tot = 1;
int fail[2600005];
int in[2600005], out[2600005], dfn[2600005], node;
vector<pair<int, int>> qu[100005];
vector<int> adj[2600005];
int ans[100005];
bool vis[2600005];
int c[2600005];
inline int lowbit(int x) {
return x & (-x);
}
void upd(int x, int v) {
for(int i = x;i <= tot;i += lowbit(i)) {
c[i] += v;
}
}
int que(int x) {
int res = 0;
for(int i = x;i > 0;i -= lowbit(i)) {
res += c[i];
}
return res;
}
void ins() {
int p = rt;
for(int i = 1, m = strlen(str + 1);i <= m;i++) {
if(str[i] == 'B') {
p = father[p];
}
else if(str[i] == 'P') {
pos[p] = ++n;
ed[n] = p;
}
else {
int ch = str[i] - 'a';
if(trie[p][ch] == 0) {
trie[p][ch] = ++tot;
}
father[trie[p][ch]] = p, p = trie[p][ch];
}
}
}
void buildFail() {
queue<int> que;
for(int ch = 0;ch < 26;ch++) {
if(trie[rt][ch] != 0) {
que.push(trie[rt][ch]);
}
else {
trie[rt][ch] = rt;
}
fail[trie[rt][ch]] = rt;
}
while(!que.empty()) {
int u = que.front(); que.pop();
for(int ch = 0;ch < 26;ch++) {
if(trie[u][ch] != 0) {
fail[trie[u][ch]] = trie[fail[u]][ch];
que.push(trie[u][ch]);
}
else {
trie[u][ch] = trie[fail[u]][ch];
}
}
}
}
void dfs(int u) {
if(vis[u] == true) {
return;
}
vis[u] = true;
dfn[u] = ++node;
in[u] = node;
for(int v: adj[u]) {
dfs(v);
}
out[u] = node;
}
int main() {
ios::sync_with_stdio(false);
cin.tie(nullptr), cout.tie(nullptr);
cin >> (str + 1);
ins();
buildFail();
for(int i = 1;i <= tot;i++) {
adj[fail[i]].push_back(i);
}
dfs(rt);
cin >> q;
for(int i = 1;i <= q;i++) {
int x, y;
cin >> x >> y;
qu[y].push_back(make_pair(x, i));
}
int p = rt;
for(int i = 1, m = strlen(str + 1);i <= m;i++) {
if(str[i] == 'B') {
upd(dfn[p], -1); p = father[p];
}
else if(str[i] == 'P') {
for(pair<int, int> j: qu[pos[p]]) {
ans[j.second] = que(out[ed[j.first]]) - que(in[ed[j.first]] - 1);
}
}
else {
int ch = str[i] - 'a';
upd(dfn[trie[p][ch]], +1); p = trie[p][ch];
}
}
for(int j = 1;j <= q;j++) {
cout << ans[j] << '\n';
}
cout.flush();
return 0;
}
P3715 [BJOI2017] 魔法咒语
$L\leq 100$ 时,我们设 $dp_{i,j}$ 表示前 $i$ 个字符,在 AC 自动机上走到 $j$ 节点的方案数。
我们一次直接转移一个基本词汇,转移需要注意 $trie_{j,ch}$ 不能是被禁的咒语。
$L\leq 10^8$ 时,观察到词汇长度不超过 $2$,那么由 $dp_i$ 只会转移至 $dp_{i+1}$ 和 $dp_{i+2}$,第二维转移与第一维无关,预处理 $[dp_{i-1},dp_i]$ 的转移矩阵做矩阵乘法即可。
时间复杂度 $\mathcal{O}(|S|\cdot26+(2|S|)^3\log L)$。
代码
#include <bits/stdc++.h>
using namespace std;
const int Mod = 1000000007;
int n, m, L;
int len[55], mxlen;
char word[55][105];
char str[105];
int trie[105][26], rt = 1, tot = 1;
int fail[2605];
bool vis[2605];
void ins() {
int p = rt;
for(int i = 1, l = strlen(str + 1);i <= l;i++) {
int ch = str[i] - 'a';
if(trie[p][ch] == 0) {
trie[p][ch] = ++tot;
}
p = trie[p][ch];
}
vis[p] = true;
}
void buildFail() {
queue<int> que;
for(int ch = 0;ch < 26;ch++) {
if(trie[rt][ch] != 0) {
que.push(trie[rt][ch]);
}
else {
trie[rt][ch] = rt;
}
fail[trie[rt][ch]] = rt;
}
while(!que.empty()) {
int u = que.front(); que.pop();
for(int ch = 0;ch < 26;ch++) {
if(trie[u][ch] != 0) {
fail[trie[u][ch]] = trie[fail[u]][ch]; vis[trie[u][ch]] |= vis[fail[trie[u][ch]]];
que.push(trie[u][ch]);
}
else {
trie[u][ch] = trie[fail[u]][ch];
}
}
}
}
void upd(int &a, int b) {
a += b;
if(a >= Mod) {
a -= Mod;
}
}
namespace SubTask1 {
int ans;
int F[205], G[205];
struct Mat {
int num[205][205];
Mat() {
memset(num, 0, sizeof(num));
}
Mat operator * (const Mat &A) {
Mat res;
for(int i = 1;i <= 2 * tot;i++) {
for(int j = 1;j <= 2 * tot;j++) {
for(int k = 1;k <= 2 * tot;k++) {
upd(res.num[i][j], 1ll * num[i][k] * A.num[k][j] % Mod);
}
}
}
return res;
}
};
Mat Matpow(Mat A, int b) {
Mat base = A, res;
for(int i = 1;i <= 2 * tot;i++) {
res.num[i][i] = 1;
}
while(b) {
if(b & 1) res = res * base;
b >>= 1;
base = base * base;
}
return res;
}
int move(int p, int k) {
for(int i = 1;i <= len[k];i++) {
int ch = word[k][i] - 'a';
if(vis[trie[p][ch]] == true) {
return -1;
}
p = trie[p][ch];
}
return p;
}
void sol() {
Mat A, B;
for(int p = 1;p <= tot;p++) {
for(int k = 1;k <= n;k++) {
int q = move(p, k);
if(q == -1) {
continue;
}
if(len[k] == 1) {
A.num[q + tot][p + tot]++;
}
else {
A.num[q + tot][p]++;
}
}
}
for(int p = 1;p <= tot;p++) {
A.num[p][p + tot] = 1;
}
B = Matpow(A, L - 1);
F[rt] = 1;
for(int k = 1;k <= n;k++) {
if(len[k] == 1) {
int ch = word[k][1] - 'a';
if(vis[trie[rt][ch]] == false) {
F[tot + trie[rt][ch]]++;
}
}
}
for(int i = 1;i <= 2 * tot;i++) {
for(int k = 1;k <= 2 * tot;k++) {
upd(G[i], 1ll * B.num[i][k] * F[k] % Mod);
}
}
for(int i = tot + 1;i <= 2 * tot;i++) {
upd(ans, G[i]);
}
cout << ans << '\n';
}
}
namespace SubTask2 {
int dp[105][2605], ans;
void sol() {
dp[0][rt] = 1;
for(int i = 0;i < L;i++) {
for(int j = 1;j <= tot;j++) {
if(dp[i][j] == 0) {
continue;
}
for(int k = 1;k <= n;k++) {
if(i + len[k] > L) {
continue;
}
int j0 = j;
bool flag = true;
for(int q = 1;q <= len[k];q++) {
int ch = word[k][q] - 'a';
if(vis[trie[j0][ch]] == true) {
flag = false; break;
}
j0 = trie[j0][ch];
}
if(flag == false) {
continue;
}
upd(dp[i + len[k]][j0], dp[i][j]);
}
}
}
for(int j = 1;j <= tot;j++) {
upd(ans, dp[L][j]);
}
cout << ans << '\n';
}
}
int main() {
ios::sync_with_stdio(false);
cin.tie(nullptr), cout.tie(nullptr);
cin >> n >> m >> L;
for(int i = 1;i <= n;i++) {
cin >> (word[i] + 1);
len[i] = strlen(word[i] + 1);
mxlen = max(mxlen, len[i]);
}
for(int i = 1;i <= m;i++) {
cin >> (str + 1);
ins();
}
buildFail();
if(mxlen <= 2) {
SubTask1::sol();
}
else {
SubTask2::sol();
}
cout.flush();
return 0;
}
后面的题感觉都差不多。。。就不写了