有向图强联通分量/无向图割点割边

By WyyOIer |

2022-12-24 18:21:30 /

2023-01-11 13:54:25

阅读数 nan

有向图强联通分量

概念

强联通分量 $\text{(Strongly Connected Component, SCC)}$

如果有向图中任意两点都有相互可达的路径，则称此图为强联通图。

一个极大的强联通子图称为图的强联通分量。

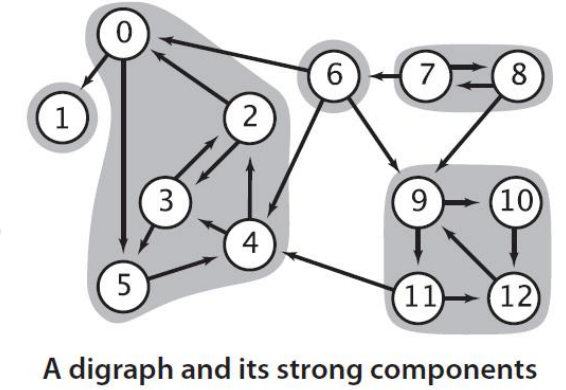
边的分类

有向图中将边分为如下几类：

树边：图上 dfs 树上的边。
后向边：dfs 树上后代指向祖先的边。
前向边：dfs 树上祖先指向后代的边但不包括树边。
交叉边：其它边，边的两个节点没有祖先后代关系。

算法流程

那么我们如何求出一个图的所有强联通分量？

我们定义 $dfn_u$ 为通过树边走到 $u$ 节点的时间戳，$low_u$ 表示从 $u$ 子树节点出发，走一条交叉边或后向边可以到达 $v$ 的 $dfn_v$ 最小值，且 $v$ 可通过若干条边到达 $u$。

当我们 dfs 走到 $u$ 时，令 $dfn_u=low_u$，并遍历边 $(u,v)$：

后向边：我们通过一条后向边走到 $v$，且 $v$ 可到达 $u$，那么更新 $low_u=\min(low_u,dfn_v)$。
交叉边：如果 $v$ 能够到达 $u$，则可以更新 $low_u=\min(low_u,dfn_v)$。
树边：子树内的所有点都可作为 $u$ 的贡献，因此更新为 $low_u=\min(low_u,low_v)$。
前向边：不会存在前向边。

为了判断交叉边的 $v$ 是否能到达 $u$，我们用栈记录在 $u$ 之前遍历的点，那么栈内中存在的点即为所有能够到达 $u$ 的点。

如果最终 $dfn_u=low_u$，那么 $u$ 无法回到比它时间戳小的节点，那么它就是一个强联通分量的根，此时将栈顶依次弹出，直到 $u$ 为止，这就是原图中的一个强连通分量。

int n, m;
vector<int> adj[100005];
int scc[100005], color;
int stac[100005], top;
bool inst[100005]; // 记录节点是否在栈内
int dfn[100005], low[100005], node;

void tarjan(int u) {
    dfn[u] = low[u] = ++node;
    stac[++top] = u; inst[u] = true;
    for(int v: adj[u]) {
        if(dfn[v] == 0) { // 树边
            tarjan(v);
            low[u] = min(low[u], low[v]);
        }
        else if(inst[v] == true) { // 后向边或交叉边
            low[u] = min(low[u], dfn[v]);
        }
    }
    if(dfn[u] == low[u]) {
        ++color;
        while(true) {
            int v = stac[top]; top--;
            inst[v] = false;
            scc[v] = color; // 标记强联通分量
            if(v == u) break;
        }
    }
}

定理

将原有向图按强联通分量缩点（即将强联通分量中的所有节点看作一个点）后，原图形成了一个有向无环图。
缩点后的 DAG 中唯一出度为 $0$ 的点，则从任意点出发均可到达这个强连通分量对应的点。
缩点后的 DAG 所有入度不为 $0$ 的点，一定可以由某个入度为 $0$ 的点出发可达。

无向图割点割边

概念

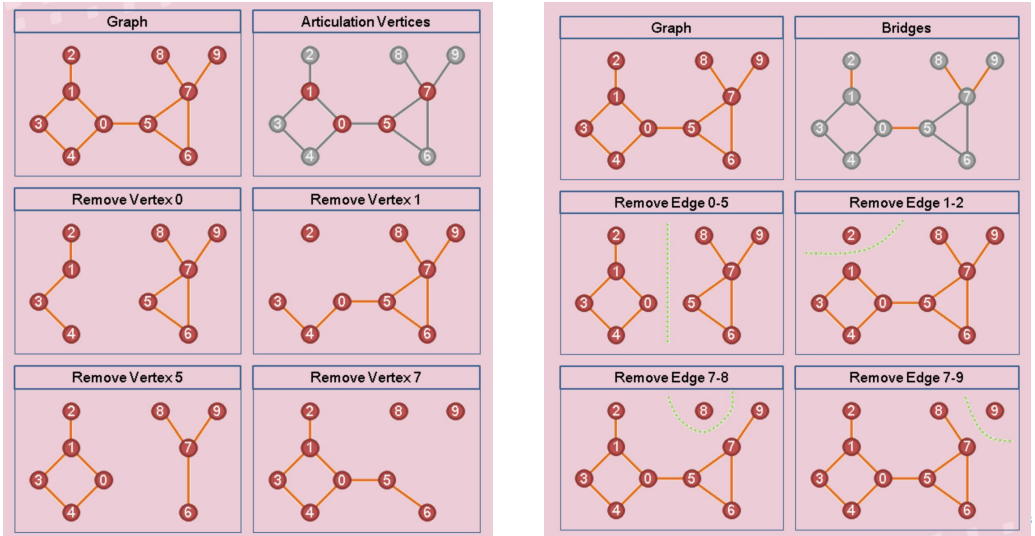
割点 $\text{(Cut Vertex)}$

在无向联通图中，如果删除某点后，图变成不联通，称该点为割点。

割边 $\text{(Cut Edge, Bridge)}$

在无向联通图中，如果删除某边后，图变成不联通，称该边为割边。

算法流程

由于无向图中不存在前向边和交叉边，那么此时的 $low_u$ 重定义为 $u$ 子树节点出发通过一条后向边走到的 $v$ 的 $dfn_v$ 最小值。

那么割点和割边如何判断。

对于割点来说，当且仅当满足下列条件中的一个：

$u$ 是 dfs 树的根节点，求 $u$ 有多于一个子树。（注意不是有多条边而是多条树边）
$dfn_u\leq low_v$，那么删去 $u$ 后，$v$ 及其子树无法回到 $u$ 以上的节点，则原图变为不联通。

对于割边来说，需要满足 $dfn_u<low_v$，即删去边 $(u,v)$ 后，$v$ 及其子树无法回到 $u$ 以及 $u$ 以上的节点，则原图不联通，注意 $dfn_u$ 不可以等于 $low_v$，如果等于则删去 $(u,v)$ 后 $v$ 还可以通过后向边回到 $u$，则原图仍然联通。

因此也可以看出割边一定是树边，若图中有重边，则这条边也不会是割边，注意判断。

int n, m;
vector<int> adj[100005];
map<int, int> edge; // 若有重边需要使用 map 判断
int father[100005]; // 记录树边的 father
int dfn[100005], low[100005], node;
bool cv[100005]; // cut vertex 割点
bool ce[100005]; // cut edge 割边   
// 由于必须是树边，则此时 ce[i] 表示的是 (i, father[i]) 是否为割边

void tarjan(int u, int fa) {
    father[u] = fa;
    dfn[u] = low[u] = ++node;
    for(int v: adj[u]) {
        if(dfn[v] == 0) { // 树边
            tarjan(v, u);
            low[u] = min(low[u], low[v]);
            if(dfn[u] < low[v] && edge[make_pair(u, v)] <= 1 && edge[make_pair(v, u)] <= 1) {
                ce[v] = true; // (v, u) 为割边
            }
            if(dfn[u] <= low[v]) {
                cv[u] = true;
            }
        }
        else if(v != fa) { // 非树边
            low[u] = min(low[u], dfn[v]);
        }
    }
}

int main() {
    /*   main() 函数中关于割点割边的预处理   */
    for(int i = 1; i <= m; i++) {
        int u, v;
        cin >> u >> v;
        adj[u].push_back(v);
        adj[v].push_back(u);
        edge[make_pair(u, v)]++;
        edge[make_pair(v, u)]++;
    }
    for(int i = 1; i <= n; i++) {
        if(dfn[i] == 0) {
            tarjan(i, 0);
            int cnt = 0;
            for(int v: adj[i]) {
                if(father[v] == i) {
                    cnt++;
                }
            }
            cv[i] = (cnt > 1);
        }
    }
}

点双联通分量/边双联通分量

概念

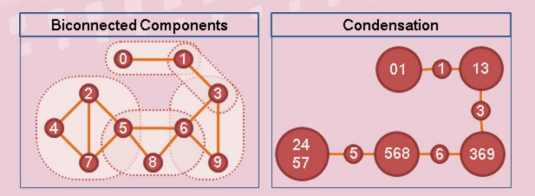
点双联通分量 $\text{(Biconnected Components, vcc)}$

一个极大的不存在割点的分量，称为点双联通分量。

每条边属于一个点双。

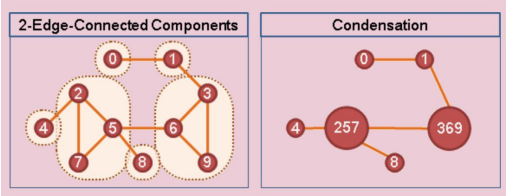
边双联通分量 $\text{(2-Edge-Connected Components, ecc)}$

一个极大的不存在割边的分量，称为边双联通分量。

每个点属于一个边双。

圆方树

对于图中的每一个点双，我们做如下的操作：

点双中的每个点看作圆点，新建一个方点；
拆掉原点双中的边
每个圆点向其方点连一条边。

容易证明形成了一个树形结构，称之为圆方树。

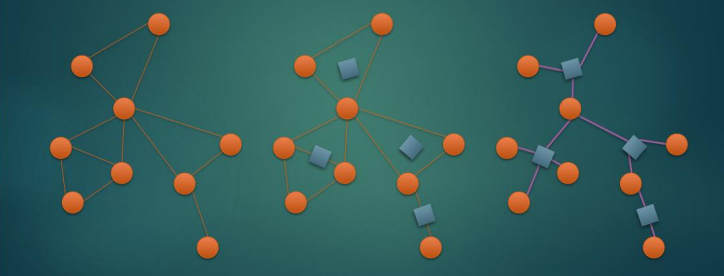
圆方树.png

算法流程

主要说一下圆方树的建法。

我们在 dfs 同时也要再去维护一个栈，当我们找到割点 $u$ 时，弹出栈顶的点直到 $u$ 但保留 $u$ 在栈内，因为 $u$ 同时还会构成其它的点双，因此还会连边。

int Ver;
vector<int> adj[100005], RST[200005];
int stac[100005], top;
int dfn[100005], low[100005], node;

void tarjan(int u, int fa) {
    dfn[u] = low[u] = ++node;
    stac[++top] = u;
    for(int v: adj[u]) {
        if(dfn[v] == 0) {
            tarjan(v, u);
            low[u] = min(low[u], low[v]);
            if(dfn[u] <= low[v]) {
                ++Ver;
                while(true) {
                    int g = stac[top]; top--;
                    RST[Ver].push_back(g);
                    RST[g].push_back(Ver);
                    if(g == v) break;
                }
                RST[Ver].push_back(u);
                RST[u].push_back(Ver);
            }
        }
        else if(v != fa) {
            low[u] = min(low[u], dfn[v]);
        }
    }
}

性质

圆方树中与圆点相连的点一定是方点，与方点相连的点一定是圆点。
点双建圆方树后，两点 $(u,v)$ 路径上必经之点就是圆方树上路径圆点数量，也等于 $\dfrac{dist}{2}+1$。
边双一定是一棵树。
一个节点属于多个点双等价于这个节点是割点。同时在圆方树中，这个点的度数大于 $1$。

习题

P2341 [USACO03FALL / HAOI2006] 受欢迎的牛 G

如果将喜欢关系看作一条有向边，对于某一点，如果所有点都可到达这个点，则这个点对应的奶牛是明星。

根据上述结论，将有向图缩点后看出度为 $0$ 的强联通分量数量，若大于 $1$ 个，则没有明星奶牛，否则，唯一的一个出度为 $0$ 的强联通分量的所有奶牛都是明星奶牛。

时间复杂度 $\mathcal{O}(n)$。

代码

#include <bits/stdc++.h>

using namespace std;

int n, m;
vector<int> adj[10005];

int dfn[10005], low[10005], node;
bool inst[10005];
int stac[10005], top;
int scc[10005], color, outDeg[10005];
int bucket[10005];

void tarjan(int u) {
    dfn[u] = low[u] = ++node;
    stac[++top] = u; inst[u] = true;
    for(int v: adj[u]) {
        if(dfn[v] == 0) {
            tarjan(v);
            low[u] = min(low[u], low[v]);
        }
        else if(inst[v] == true) {
            low[u] = min(low[u], dfn[v]);
        }
    }
    if(low[u] == dfn[u]) {
        ++color;
        while(true) {
            int v = stac[top]; top--;
            inst[v]	= false;
            scc[v] = color;
            if(v == u) {
                break; 
            }
        }
    }
}


int main() {
    ios::sync_with_stdio(false);
    cin.tie(nullptr), cout.tie(nullptr);
    
    cin >> n >> m;
    for(int i = 1;i <= m;i++) {
        int u, v;
        cin >> u >> v;
        adj[u].push_back(v);
    }
    for(int i = 1;i <= n;i++) {
        if(dfn[i] == 0) {
            tarjan(i);
        }
    }
    for(int u = 1;u <= n;u++) {
        bucket[scc[u]]++;
        for(int v: adj[u]) {
            if(scc[u] != scc[v]) {
                outDeg[scc[u]]++;
            }
        }
    }
    int cnt = 0, p = 0;
    for(int i = 1;i <= color;i++) {
        if(outDeg[i] == 0) {
            cnt++; p = i;
        }
    }
    if(cnt > 1) {
        cout << "0\n";
    }
    else {
        cout << bucket[p] << '\n';
    }
    
    cout.flush();
    return 0;
}

P3387 【模板】缩点

由于一个强联通分量内的点互相可达，因此我们将强联通分量缩点并挂上联通分量内的点权之和，由于缩完点后的图是个 DAG，直接拓扑序跑 dp 即可。

P2272 [ZJOI2007]最大半连通子图

由半联通子图的定义可知，我们在缩点的图上选一条链即可。方案数可以在求最大值的时候同时统计。（参考最短路计数）

注意要去掉重边。

代码

#include <bits/stdc++.h>

using namespace std;

int n, m, p;
vector<int> adj[2][100005];
map<pair<int, int>, bool> edge;
int scc[100005], color;
int stac[100005], top;
bool inst[100005];
int dfn[100005], low[100005], node;
int inDeg[100005];
int bucket[100005], f[100005], g[100005];
int ans1, ans2;

void upd(int &a, int b) {
    a += b;
    if(a >= p) {
        a -= p;
    }
}

void tarjan(int u) {
    dfn[u] = low[u] = ++node;
    stac[++top] = u; inst[u] = true;
    for(int v: adj[0][u]) {
        if(dfn[v] == 0) {
            tarjan(v);
            low[u] = min(low[u], low[v]);
        }
        else if(inst[v] == true) {
            low[u] = min(low[u], dfn[v]);
        }
    }
    if(dfn[u] == low[u]) {
        ++color;
        while(true) {
            int v = stac[top]; top--;
            inst[v] = false;
            scc[v] = color;
            if(u == v) break;
        }
    }
}

void topo() {
    queue<int> que;
    for(int i = 1;i <= color;i++) {
        if(inDeg[i] == 0) {
            que.push(i); f[i] = bucket[i], g[i] = 1;
        }
    }
    while(!que.empty()) {
        int u = que.front(); que.pop();
        
        for(int v: adj[1][u]) {
            if(f[v] < f[u] + bucket[v]) {
                f[v] = f[u] + bucket[v], g[v] = g[u];
            }
            else if(f[v] == f[u] + bucket[v]) {
                upd(g[v], g[u]);
            }
            inDeg[v]--;
            if(inDeg[v] == 0) {
                que.push(v);
            }
        }
    }
}

int main() {
    ios::sync_with_stdio(false);
    cin.tie(nullptr), cout.tie(nullptr);
    
    cin >> n >> m >> p;
    for(int i = 1;i <= m;i++) {
        int u, v;
        cin >> u >> v;
        adj[0][u].push_back(v);
    }
    for(int i = 1;i <= n;i++) {
        if(dfn[i] == 0) {
            tarjan(i);
        }
    }
    for(int u = 1;u <= n;u++) {
        bucket[scc[u]]++;
        for(int v: adj[0][u]) {
            if(scc[u] != scc[v] && edge[make_pair(scc[u], scc[v])] == false) {
                edge[make_pair(scc[u], scc[v])] = true;
                adj[1][scc[u]].push_back(scc[v]);
                inDeg[scc[v]]++;
            }
        }
    }
    topo();
    for(int i = 1;i <= color;i++) {
        if(ans1 < f[i]) {
            ans1 = f[i], ans2 = g[i];
        }
        else if(ans1 == f[i]) {
            upd(ans2, g[i]);
        }
    }
    cout << ans1 << '\n' << ans2 << '\n';
    cout.flush();
    return 0;
}

P5058 [ZJOI2004] 嗅探器

可以观察到嗅探器应该安装在两点之间的割点上。那么我们可以建出圆方树，然后看两点间编号最小的节点。

代码

#include <bits/stdc++.h>

using namespace std;
const int I = 0x3f3f3f3f;

int n, s, t;
int Ver;
vector<int> adj[200005], RST[400005];
int stac[200005], top;
int dfn[200005], low[200005], node;

void tarjan(int u, int fa) {
    dfn[u] = low[u] = ++node;
    stac[++top] = u;
    for(int v: adj[u]) {
        if(dfn[v] == 0) {
            tarjan(v, u);
            low[u] = min(low[u], low[v]);
            if(dfn[u] <= low[v]) {
                ++Ver;
                while(true) {
                    int q = stac[top]; top--;
                    RST[Ver].push_back(q);
                    RST[q].push_back(Ver);
                    if(q == v) break;
                }
                RST[Ver].push_back(u);
                RST[u].push_back(Ver);
            }
        }
        else if(v != fa) {
            low[u] = min(low[u], dfn[v]);
        }
    }
}

void dfs(int u, int fa, int tot) {
    if(u == t) {
        if(tot == I) {
            cout << "No solution\n";
        }
        else {
            cout << tot << '\n';
        }
        exit(0);
    }
    if(u != s && u <= n) {
        tot = min(tot, u);
    }
    for(int v: RST[u]) {
        if(v == fa) {
            continue;
        }
        dfs(v, u, tot);
    }
}


int main() {
    ios::sync_with_stdio(false);
    cin.tie(nullptr), cout.tie(nullptr);
    
    cin >> n; Ver = n;
    int u, v;
    while(cin >> u >> v && (u + v) > 0) {
        adj[u].push_back(v);
        adj[v].push_back(u);
    }
    cin >> s >> t;
    tarjan(s, 0);
    if(dfn[t] == 0) {
        cout << "No solution\n";
    }
    else {
        dfs(s, 0, I);
    }
    
    cout.flush();
    return 0;
}

P8867 [NOIP2022] 建造军营

被疫情鸽掉的一次联赛，还好没考，不然就还没学点双。

既然是一道联赛题，我们还是以完整的流程观察这道题。

首先思考从何入手，我们可以看这句话：

而此时 A 国接到情报，B 国将会于不久后袭击 A 国的一条道路，但具体的袭击目标却无从得知。如果 B 国袭击成功，这条道路将被切断，可能会造成 A 国某两个军营无法互相到达，这是 A 国极力避免的。

观察到加粗文字就是割边的定义，且 B 国只会袭击一条道路，那么这就引导我们往割边方向考虑。

所以现在我们得知：当 B 国切掉割边后，A 国不联通，那么 A 国就需要保护这些割边，其它的边是什么情况暂时还没有头绪，且本题中我们还要考虑城市选择的情况。但是考虑到缩完点双后有向图变为树，不妨使用树形 dp 求方案数。

（以下的 dp 所涉及的子树基于缩了点双后的树形结构定义）

记 $dp_{u,0/1}$ 表示 $u$ 子树内没选任何点/选了一个以 $u$ 为连通块的方案数并强制不选择 $(u,fa_u)$ 的方案数（避免在 $dp_{fa_u,0/1}$ 时统计重复），$e_u$ 为 $u$ 子树内的边数（原图上的边数），$sz_u$ 为树上节点 $u$（边双）的点数和边数数量之和（原图的点数和边数）。

当 $u$ 子树没选任何点时，则切断 $u$ 子树的任意边都不会影响联通情况，故 A 国随意钦定即可，$dp_{u,0}=2^{e_u}$。
当 $u$ 子树选了一个以 $u$ 为根的联通块时，$u$ 节点内由点双性质，删除任意一条边仍然连通，故可随意钦定；考虑 $u$ 的儿子 $v$，当 $v$ 中没选点，$(u,v)$ 可选可不选，贡献 $2$ 种情况，当 $v$ 选点，因 $(u,v)$ 是割边，则必选，贡献 $1$ 种情况。但是上述讨论并没有排除 $u$ 子树内中没有选点的情况，因此需要减去，最终转移方程 $dp_{u,1}=2^{sz_u}\prod(2dp_{v,0}+dp_{v,1})-dp_{u,0}$。

做到这里就可以兴奋的做最后一步：统计答案，答案即为 $\sum dp_{u,1}\times 2^{m-e_u-[u\neq 1]}$。（联通块根节点不为 $1$ 时，强制不选 $(u,fa_u)$，因此减 $1$）

时间复杂度 $\mathcal{O}(n)$，用到了边双和基于边双概念定义的树形 dp，我认为思维难度大致与 [NOIP2021] 数列相同。

代码

#include <bits/stdc++.h>

using namespace std;
const int Mod = 1000000007;

int n, m;
vector<int> adj[2][500005];

int pow2[1500005];
int father[500005];

int dfn[500005], low[500005], node;
bool ce[500005];

int ecc[500005], color;
int e[500005], sz[500005];
int dp[500005][2], ans;

void add(int &a, int b) {
    a += b;
    if(a >= Mod) {
        a -= Mod;
    }
    if(a < 0) {
        a += Mod;
    }
}

void mul(int &a, int b) {
    a = 1ll * a * b % Mod;
}

void tarjan(int u, int fa) {
    father[u] = fa;
    dfn[u] = low[u] = ++node;
    for(int v: adj[0][u]) {
        if(dfn[v] == 0) {
            tarjan(v, u);
            low[u] = min(low[u], low[v]);
            if(dfn[u] < low[v]) {
                ce[v] = true;
            }
        }
        else if(v != fa) {
            low[u] = min(low[u], dfn[v]);
        }
    }
}

void dfs1(int u, int c) {
    ecc[u] = c;
    for(int v: adj[0][u]) {
        if((ce[u] == true || ce[v] == true) && (v == father[u] || u == father[v])) {
            continue;
        }
        if(ecc[v] == 0) {
            dfs1(v, c);
        }
    }
}

void dfs2(int u, int fa) {
    dp[u][1] = pow2[sz[u]];
    for(int v: adj[1][u]) {
        if(v == fa) {
            continue;
        }
        dfs2(v, u);
        mul(dp[u][1], 2ll * dp[v][0] % Mod + dp[v][1]);
        e[u] += e[v] + 1;
    }
    dp[u][0] = pow2[e[u]];
    add(dp[u][1], -dp[u][0]);
    
    add(ans, 1ll * dp[u][1] * pow2[m - e[u] - (u != 1)] % Mod);
}

int main() {
    ios::sync_with_stdio(false);
    cin.tie(nullptr), cout.tie(nullptr);
    
    cin >> n >> m;
    pow2[0] = 1;
    for(int i = 1;i <= n + m;i++) {
        pow2[i] = 1ll * pow2[i - 1] * 2 % Mod;
    }
    for(int i = 1;i <= m;i++) {
        int u, v;
        cin >> u >> v;
        adj[0][u].push_back(v);
        adj[0][v].push_back(u);
    }
    tarjan(1, 0);
    for(int i = 1;i <= n;i++) {
        if(ecc[i] == 0) {
            dfs1(i, ++color);
        }
    }
    for(int i = 1;i <= n;i++) {
        sz[ecc[i]]++;
    }
    for(int u = 1;u <= n;u++) {
        for(int v: adj[0][u]) {
            if(u < v && ecc[u] == ecc[v]) {
                sz[ecc[u]]++, e[ecc[u]]++;
            }
        }
    }
    for(int i = 1;i <= n;i++) {
        if(ce[i] == true) {
            adj[1][ecc[father[i]]].push_back(ecc[i]);
            adj[1][ecc[i]].push_back(ecc[father[i]]);
        }
    }
    dfs2(1, 0);
    cout << ans << '\n';
    
    cout.flush();
    return 0;
}

P3469 [POI2008] BLO-Blockad

分情况讨论一下：

如果不是割点，则删掉与它相邻的边后，其它点仍联通，答案 $2(n-1)$。
如果是割点考虑它在搜索树上的位置，贡献即为树上断掉这个点的边后，子树之间，子树之外的贡献就会产生贡献。

所以可以在求割点的时候顺便维护信息，时间复杂度 $\mathcal{O}(n)$。

代码

#include <bits/stdc++.h>

using namespace std;
typedef long long ll;

int n, m;
int Ver;
vector<int> adj[100005];
int stac[100005], top;
int dfn[100005], low[100005], node;
ll sz[100005], ans[100005];

void tarjan(int u, int fa) {
    ll sum = 0, cnt = 0;
    sz[u] = 1;
    dfn[u] = low[u] = ++node;
    stac[++top] = u;
    for(int v: adj[u]) {
        if(dfn[v] == 0) {
            tarjan(v, u);
            low[u] = min(low[u], low[v]);
            sz[u] += sz[v];
            if(dfn[u] <= low[v]) {
                sum += sz[v];
                ans[u] += sz[v] * (n - sz[v]);
                cnt++;
            }
        }
        else if(v != fa) {
            low[u] = min(low[u], dfn[v]);
        }
    }
    if((u == 1 && cnt <= 1) || (u != 1 && cnt == 0)) ans[u] = 2 * n - 2;
    else ans[u] += (n - sum - 1) * (sum + 1) + n - 1;
}

int main() {
    ios::sync_with_stdio(false);
    cin.tie(nullptr), cout.tie(nullptr);
    
    cin >> n >> m;
    for(int i = 1;i <= m;i++) {
        int u, v;
        cin >> u >> v;
        adj[u].push_back(v);
        adj[v].push_back(u);
    }
    tarjan(1, 0);
    for(int i = 1;i <= n;i++) {
        cout << ans[i] << '\n';
    }
    
    cout.flush();
    return 0;
}

P4320 道路相遇

建圆方树后由圆方树性质，转化为求圆方树上两点距离。

时间复杂度 $\mathcal{O}((n+q)\log n)$。

#include <bits/stdc++.h>

using namespace std;

int n, m, q;
int Ver;
vector<int> adj[500005], RST[1000005];
int stac[500005], top;
int dfn[500005], low[500005], node;
int dep[1000005], lg2[1000005];
int anc[1000005][21];

void tarjan(int u, int fa) {
    dfn[u] = low[u] = ++node;
    stac[++top] = u;
    for(int v: adj[u]) {
        if(dfn[v] == 0) {
            tarjan(v, u);
            low[u] = min(low[u], low[v]);
            if(dfn[u] <= low[v]) {
                ++Ver;
                while(true) {
                    int g = stac[top]; top--;
                    RST[Ver].push_back(g);
                    RST[g].push_back(Ver);
                    if(g == v) break;
                }
                RST[Ver].push_back(u);
                RST[u].push_back(Ver);
            }
        }
        else if(v != fa) {
            low[u] = min(low[u], dfn[v]);
        }
    }
}

void dfs(int u, int fa) {
    dep[u] = dep[fa] + 1, anc[u][0] = fa;
    for(int j = 1;(1 << j) <= dep[u];j++) {
        anc[u][j] = anc[anc[u][j - 1]][j - 1];
    }
    for(int v: RST[u]) {
        if(v == fa) {
            continue;
        }
        dfs(v, u);
    }
}

int getlca(int u, int v) {
    if(dep[u] < dep[v]) {
        swap(u, v);
    }
    while(dep[u] > dep[v]) {
        int j = lg2[dep[u] - dep[v]];
        u = anc[u][j];
    }
    if(u == v) {
        return u;
    }
    for(int j = lg2[dep[u]];j >= 0;j--) {
        if(anc[u][j] != anc[v][j]) {
            u = anc[u][j], v = anc[v][j];
        }
    }
    return anc[u][0];
}

int main() {
    ios::sync_with_stdio(false);
    cin.tie(nullptr), cout.tie(nullptr);
    
    cin >> n >> m; Ver = n;
    lg2[0] = -1;
    for(int i = 1;i <= 2 * n;i++) {
        lg2[i] = lg2[i / 2] + 1;
    }
    for(int i = 1;i <= m;i++) {
        int u, v;
        cin >> u >> v;
        adj[u].push_back(v);
        adj[v].push_back(u);
    }
    for(int i = 1;i <= n;i++) {
        if(dfn[i] == 0) {
            tarjan(i, 0);
            dfs(i, 0);
        }
    }
    cin >> q;
    while(q--) {
        int u, v;
        cin >> u >> v;
        int lca = getlca(u, v);
        cout << (dep[u] + dep[v] - 2 * dep[lca]) / 2 + 1 << '\n';
    }
    
    cout.flush();
    return 0;
}

P4630 [APIO2018] 铁人两项

我们建出圆方树，枚举中转点 $c$，考虑统计 $s$ 和 $f$ 的选择方案。

我们不妨考虑在方点上计算贡献，取方点对应的点双大小作为 $c$ 的选择方案，而 $s$ 和 $f$ 要么在不同子树中，要么一个在子树中，一个在子树外，也可以轻易统计。

但是这样，显然方点的儿子也是方点子树内的选择方案，因此会出现重复统计的情况，这部分我们需要对于每一个圆点求出 $s$ 和 $f$ 的方案并将其容斥掉。

时间复杂度 $\mathcal{O}(n)$。

代码

#include <bits/stdc++.h>

using namespace std;
typedef long long ll;

int n, m;
int Ver;
vector<int> adj[100005], RST[200005];
int stac[100005], top;
int dfn[100005], low[100005], node;
ll sz[200005], Val[200005];
ll cnt;
ll ans;

void tarjan(int u, int fa) {
    dfn[u] = low[u] = ++node;
    stac[++top] = u;
    for(int v: adj[u]) {
        if(dfn[v] == 0) {
            tarjan(v, u);
            low[u] = min(low[u], low[v]);
            if(dfn[u] <= low[v]) {
                ++Ver;
                while(true) {
                    int q = stac[top]; top--; cnt++;
                    RST[Ver].push_back(q);
                    RST[q].push_back(Ver);
                    if(q == v) break;
                }
                RST[Ver].push_back(u);
                RST[u].push_back(Ver);
            }
        }
        else if(v != fa) {
            low[u] = min(low[u], dfn[v]);
        }
    }
}

void dfs(int M, int u, int fa) {
    Val[u] = (u <= n) ? -1 : (int)RST[u].size();
    sz[u] = (u <= n);
    for(int v: RST[u]) {
        if(v == fa) {
            continue;
        }
        dfs(M, v, u);
        sz[u] += sz[v];
        ans += Val[u] * sz[v] * (M - sz[v]);
    }
    if(u <= n) ans += Val[u] * (M - sz[u]) * (sz[u] - 1) + Val[u] * (M - sz[u]) * 2 + Val[u] * (sz[u] - 1);
    else ans += Val[u] * (M - sz[u]) * sz[u];
}

int main() {
    ios::sync_with_stdio(false);
    cin.tie(nullptr), cout.tie(nullptr);
    
    cin >> n >> m; Ver = n;
    for(int i = 1;i <= m;i++) {
        int u, v;
        cin >> u >> v;
        adj[u].push_back(v);
        adj[v].push_back(u);
    }
    for(int i = 1;i <= n;i++) {
        if(dfn[i] == 0) {
            cnt = 0;
            tarjan(i, 0);
            dfs(cnt + 1, i, 0);
        }
    }
    cout << ans << '\n';
    
    cout.flush();
    return 0;
}

CF487E Tourists

考虑建出圆方树，把方点的代价设为边双中的最小值。那么询问 $(a,b)$ 之间的最小值就变为圆方树上路径最小值，但是你发现修改并不好做。因为当你修改一个点的权值后，方点的新权值需要 $\mathcal{O}(n)$ 的时间重新寻找最小值。

对于这种情况，常规套路方法是用可重集维护方点儿子的权值，这样修改的权值，我们在可重集删除旧值并添加新值，就能以 $\mathcal{\log n}$ 的时间维护，最好我们上树剖来维护路径最小值，总时间复杂度 $\mathcal{O}(n\log^2 n)$。

注意当 $(a,b)$ 的最近公共祖先为方点时，实际上方点的父亲属于这个边双，我们需要同时与这个点权值取最小值。

代码

#include <bits/stdc++.h>

using namespace std;

int n, m, q;
int Ver;
int a[100005];
vector<int> adj[100005];
vector<int> RST[200005];
int stac[100005], top;
int dfn[200005], low[100005], node;
int dep[200005], father[200005], sz[200005], son[200005];
int Top[200005], pos[200005];

multiset<int> s[200005];

int tree[800005];

inline int ls(int p) {return p << 1;}
inline int rs(int p) {return p << 1 | 1;}

void pushup(int p) {
    tree[p] = min(tree[ls(p)], tree[rs(p)]);
}

void build(int p, int l, int r) {
    if(l == r) {
        tree[p] = (pos[l] > n) ? *s[pos[l]].begin() : a[pos[l]];
        return;
    }
    int mid = (l + r) >> 1;
    build(ls(p), l, mid), build(rs(p), mid + 1, r);
    pushup(p);
}

void upd(int p, int l, int r, int x, int v) {
    if(l == r) {
        tree[p] = v;
        return;
    }
    int mid = (l + r) >> 1;
    if(x <= mid) {
        upd(ls(p), l, mid, x, v);
    }
    else {
        upd(rs(p), mid + 1, r, x, v);
    }
    pushup(p);
}

int que(int p, int l, int r, int ql, int qr) {
    if(l == ql && r == qr) {
        return tree[p];
    }
    int mid = (l + r) >> 1;
    if(mid >= qr) {
        return que(ls(p), l, mid, ql, qr);
    }
    else if(mid + 1 <= ql) {
        return que(rs(p), mid + 1, r, ql, qr);
    }
    else {
        return min(que(ls(p), l, mid, ql, mid), que(rs(p), mid + 1, r, mid + 1, qr));
    }
}

int quePath(int u, int v) {
    int res = min(a[u], a[v]);
    while(Top[u] != Top[v]) {
        if(dep[Top[u]] < dep[Top[v]]) swap(u, v);
        res = min(res, que(1, 1, Ver, dfn[Top[u]], dfn[u]));
        u = father[Top[u]];
    }
    if(dep[u] < dep[v]) swap(u, v);
    res = min(res, que(1, 1, Ver, dfn[v], dfn[u]));
    if(v > n) {
        res = min(res, a[father[v]]);
    }
    return res;
}

void tarjan(int u, int fa) {
    dfn[u] = low[u] = ++node;
    stac[++top] = u;
    for(int v: adj[u]) {
        if(dfn[v] == 0) {
            tarjan(v, u);
            low[u] = min(low[u], low[v]);
            if(dfn[u] <= low[v]) {
                ++Ver;
                while(true) {
                    int t = stac[top]; top--;
                    RST[Ver].push_back(t);
                    RST[t].push_back(Ver);
                    if(t == v) break;
                }
                RST[Ver].push_back(u);
                RST[u].push_back(Ver);
            }
        }
        else if(v != fa) {
            low[u] = min(low[u], dfn[v]);
        }
    }
}

void dfs1(int u, int fa) {
    dep[u] = dep[fa] + 1, sz[u] = 1, father[u] = fa;
    for(int v: RST[u]) {
        if(v == fa) {
            continue;
        }
        dfs1(v, u);
        sz[u] += sz[v];
        if(sz[son[u]] < sz[v]) {
            son[u] = v;
        }
    }
}

void dfs2(int u, int Tp) {
    dfn[u] = ++node, Top[u] = Tp;
    pos[node] = u;
    if(son[u] != 0) {
        dfs2(son[u], Tp);
    }
    for(int v: RST[u]) {
        if(v == father[u] || v == son[u]) {
            continue;
        }
        dfs2(v, v);
    }
}

int main() {
    ios::sync_with_stdio(false);
    cin.tie(nullptr), cout.tie(nullptr);
    
    cin >> n >> m >> q;
    Ver = n;
    for(int i = 1;i <= n;i++) {
        cin >> a[i];
    }
    for(int i = 1;i <= m;i++) {
        int u, v;
        cin >> u >> v;
        adj[u].push_back(v);
        adj[v].push_back(u);
    }
    tarjan(1, 0);
    dfs1(1, 0);
    node = 0;
    dfs2(1, 1);
    
    for(int i = 1;i <= n;i++) {
        s[father[i]].insert(a[i]);
    }
    
    build(1, 1, Ver);
    
    while(q--) {
        char op;
        int x, y;
        cin >> op >> x >> y;
        if(op == 'C') {
            s[father[x]].erase(a[x]);
            s[father[x]].insert(y);
            upd(1, 1, Ver, dfn[father[x]], *s[father[x]].begin());
            upd(1, 1, Ver, dfn[x], y);
            a[x] = y;
        }
        else {
            cout << quePath(x, y) << '\n';
        }
    }
    
    cout.flush();
    return 0;
}