格线游走/反射容斥
By WyyOIer |
2023-03-19 10:35:04 /
2023-03-31 20:48:51
阅读数 nan

简述

请思考如下的经典问题：从原点 $(0,0)$ 开始，每一步只能向右或向上走，问走到 $A(n,m)$ 的方案数有多少？

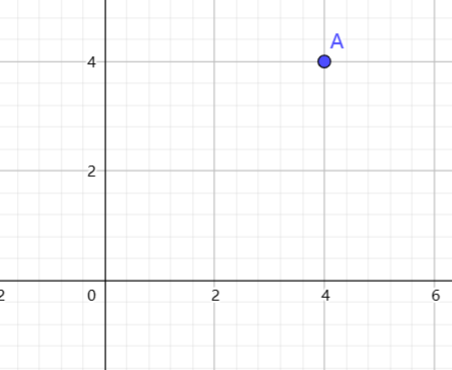
图1.png

相信大家都能一眼得出方案数为 ${n+m\choose n}$，组合意义也十分显然：将向右和向上看作 $01$ 操作，那么就是求由 $n$ 个 $0$、$m$ 个 $1$ 组成的不同 $01$ 序列数量。

这种问题就被称为格线游走的最基本形式，在这个上面有很多种拓展方法，如在其中加入障碍后询问方案数之类的，今天我们讨论其中一种拓展。

伟大的思想

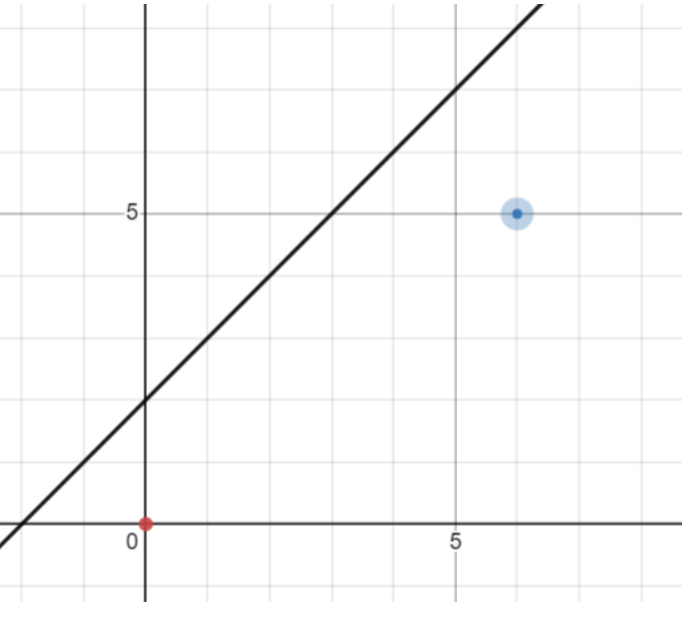
图2.png

如图，我们增添了一条直线 $y=x+b$，我们不希望碰到这条直线，那么现在的方案数是多少？

对此，我们想办法减掉经过直线后再到达终点的方案，我们可以得到点 $(n,m)$ 关于 $y=x+b$ 对称得到的点坐标为 $(m-b,n+b)$，那么我们说，每一个从 $(0,0)$ 到 $(m-b,n+b)$ 的方案都唯一对应了一个从 $(0,0)$ 先经过直线再到达终点的方案。

构造唯一对应的方法为，当第一次碰到直线时，将后面的路径对称得到原方案，显然方案之间两两不同。

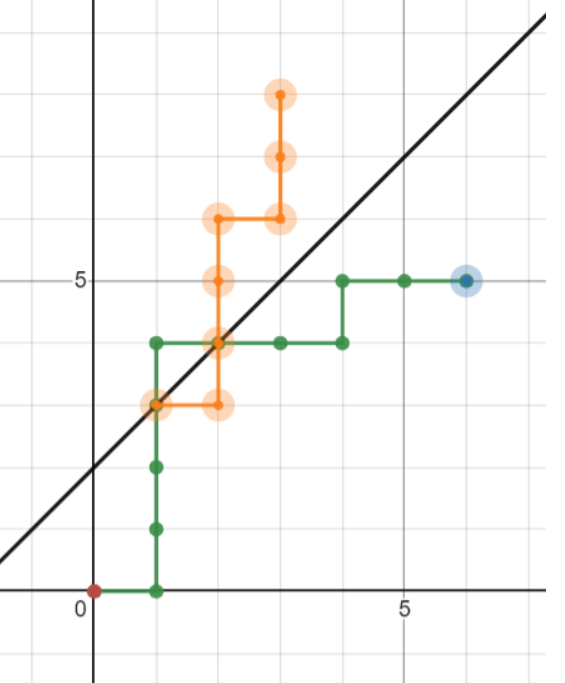
图3.png

记 $p(n,m)={n+m\choose n}$，表示 $(0,0)$ 到 $(n,m)$ 的路径数量，那么此时的答案就为 $p(n,m)-p(m-b,n+b)$。

两条直线

接下来我们考虑两条直线的情况：$y=x+b$ 与 $y=x+c$（$b>c$）

如果两条直线都在起点和终点的同一侧，即 $\min(m-n,0)>\max(b,c)$ 或 $\max(m-n,0)<\min(b,c)$，此时退化成了一条直线的情况。

我们考虑两条直线把起点和终点卡在中间的情况，即下图。

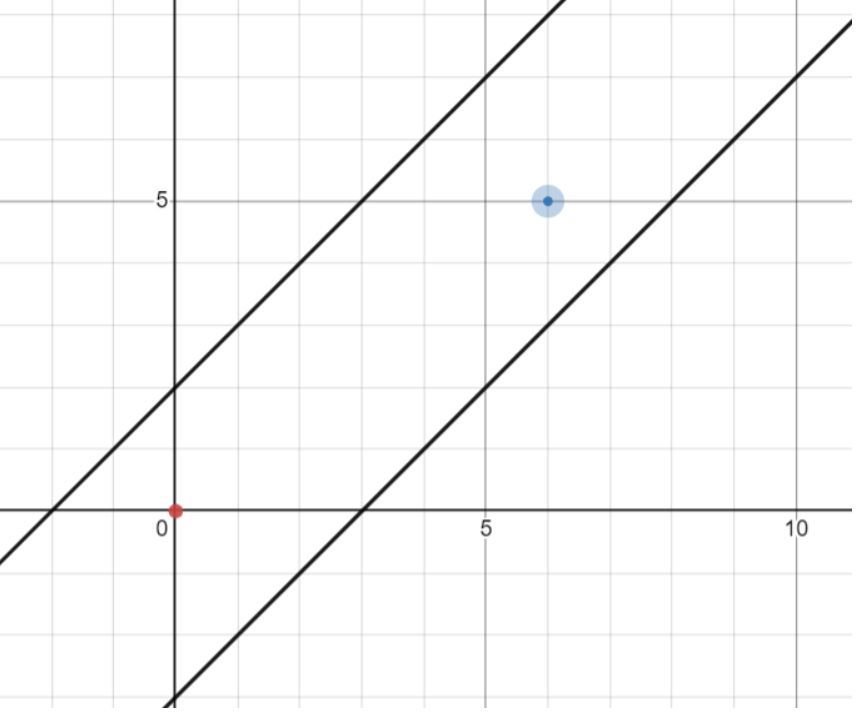
图4.png

那么我们还是利用容斥的思想：总方案数 $=$ 原方案数 $-$ 只经过 $y=x+b$ 的方案数 $-$ 只经过 $y=x+c$ 的方案数 $+$ 两条直线都经过的方案数。

这个式子是对的吗？是对的。但是想想怎么求两条直线都经过的方案数？

我们还是考虑通过翻折使之一一映射一个方案，对于一个先经过 $y=x+b$ 再经过 $y=x+c$ 再到达终点的方案：

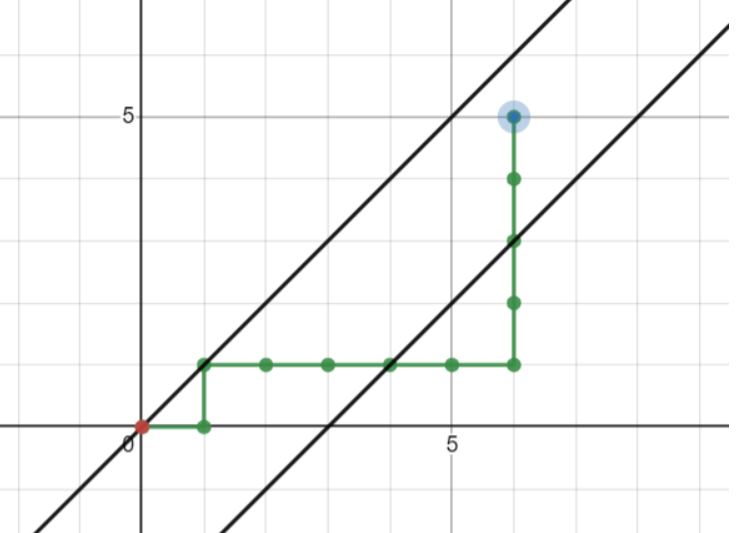
图5.png

我们在第一次经过 $y=x+b$ 时翻折，再对第一次经过 $y=x+c$ 时按 $y=x+c$ 关于 $y=x+b$ 对称后的直线（也就是 $y=x+(2b-c)$）翻折：

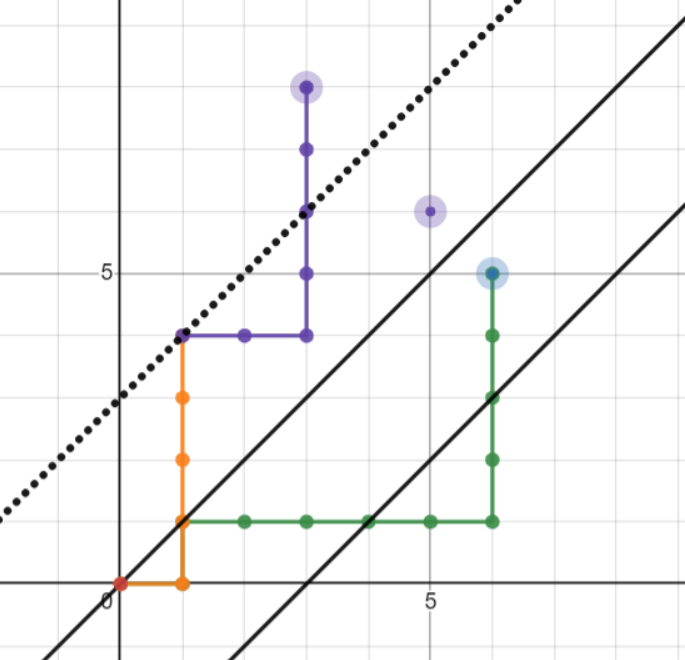
图6.png

可以说明此时从 $(0,0)$ 走到翻折后最终的点 $(n’,m’)$ 的方案一一对应了一个先走到 $y=x+b$ 再走到 $y=x+c$ 的方案。

然而还有先经过 $y=x+c$ 再经过 $y=x+b$ 的方案，先经过 $y=x+b$ 再经过 $y=x+c$ 再经过 $y=x+b$ 的路线……问题变的棘手。

反射容斥

我们需要对所有的经过直线顺序的情况进行容斥。记反射序列形如 $bcb…$ 表示格线游走依次按顺序经过直线 $y=x+b,y=x+c,y=x+b,…$ 的方案，考虑我们怎么对这种依次经过直线的方案容斥的。

每当我们第一次到达直线时，将所对应的点和直线翻折，类比下来，那么我们可以依次对经过的直线顺序翻折，最终翻折所得到终点的方案数就是以反射序列到达原终点的方案数。

我们观察反射序列的形式，发现一定是由 $b,c$ 依次交替组成的，因为我们只在碰到 $b$ 后的下一次碰到 $c$ 才翻折，或碰到 $c$ 的下一次碰到 $b$ 后才翻折，如果连续经过了 $b$ 或 $c$，可以发现我们没有对于这种情况翻折。

综上，我们可以把最终答案以容斥写成了这样一个形式：总方案 $-b-c+bc+cb-bcb-cbc+…$

我们考虑这样的项一共有多少个。由于每次反射后都有偏移，且因为 $b,c$ 交替反射，所以终点总是在往负半轴跑，当跑到非第一象限的区域时方案数为 $0$，因此之后就不用计算，最终时间复杂度为 $\mathcal{O}(\dfrac{n+m}{b-c})$。

实现

我们可以将所有反射序列看作两组：$bcbc…$ 与 $cbcb…$，我们可以同时维护这两组。

我们考虑需要实时维护什么：两条直线的截距，反射后的终点位置，那么我们可以记录 $b,c$ 分别表示两条直线截距，$(x,y)$ 表示终点坐标。

枚举反射次数，我们就能知道当前轮是 $b$ 关于 $c$ 对称还是 $c$ 关于 $b$ 对称，终点关于 $b$ 对称还是关于 $c$ 对称，然后就能求出下一轮。

inline int p(int a, int b) { // a + b = n
    if(a < 0 || b < 0) return 0;
    else return comb[a];
}

inline int d(int b, int c) { // 将 c 关于 b 对称，用于 y = x + c 关于 y = x + b 的对称
    return 2 * b - c;
}

inline pair<int, int> sym(pair<int, int> func, int b) { // 将点 (x, y) 关于函数 y = x + b 对称
    return make_pair(func.second - b, func.first + b);
}

inline bool chk(pair<int, int> func) {
    return func.first >= 0 && func.second >= 0;
}

int sol(int b, int c) {
    ll res = p(x, y);
    pair<int, int> func1 = sym(make_pair(x, y), b), func2 = sym(make_pair(x, y), c);
    int temp_b = b, temp_c = d(b, c);
    for(int i = 1; chk(func1) == true; ++i) {
        int mul = (i & 1 ? -1 : 1);
        res = (res + p(func1.first, func1.second) * mul + Mod) % Mod;
        if(i % 2 == 0) {
            func1 = sym(func1, temp_b);
            temp_c = d(temp_b, temp_c);
        }
        else {
            func1 = sym(func1, temp_c);
            temp_b = d(temp_c, temp_b);
        }
    }
    temp_b = d(c, b), temp_c = c;
    for(int i = 1; chk(func2) == true; ++i) {
        int mul = (i & 1 ? -1 : 1);
        res = (res + p(func2.first, func2.second) * mul + Mod) % Mod;
        if(i % 2 == 0) {
            func2 = sym(func2, temp_c);
            temp_b = d(temp_c, temp_b);
        }
        else {
            func2 = sym(func2, temp_b);
            temp_c = d(temp_b, temp_c);
        }
    }
    return res;
}